問題
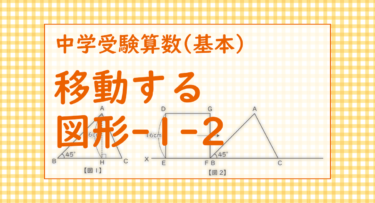
分数を次のように並べます。
![]()
(1) $ \displaystyle \frac{1}{13} $がはじめて現れるのは左はしから数えて何番目ですか。
(2) 左はしから数えて200番目の分数は何ですか。
(3) 1番目から200番目までの分数をすべて足したらいくつですか。
これまでほとんどの通信教育で実現できなかった難関国私立中学合格。Z会なら、可能です。【公立中高一貫校を受検予定 】の方は試しに資料請求してみましょう。HPにも「小学生コース専科 公立中高一貫校受検対策講座のご案内」が詳しく記載されています。
解答
- 解答を開く
-
分数を次のように並べます。

(1) $ \displaystyle \frac{1}{13} $がはじめて現れるのは左はしから数えて何番目ですか。
(2) 左はしから数えて200番目の分数は何ですか。
(3) 1番目から200番目までの分数をすべて足したらいくつですか。同じ分母を一団とする群数列として扱うと分かり易くなる。

(1)
第1群(分母1)・・・1コ
第2群(分母3)・・・3コ
第3群(分母5)・・・5コ
第4群(分母7)・・・7コ
第5群(分母9)・・・9コ
第6群(分母11)・・・11コ
第7群(分母13)・・・13コ
これより、1+3+5+7+9+11+1=37(答え) 37番目
(2)
1,3,5,…,nの和がはじめて200を超えるn(第n群)を求める。
1+3+5+7+9+11+13+15+17+19+21+23+25+27=196
第14群までの分数の数が196コとなるので、第15群($ \displaystyle \frac{1}{29} $ $ \displaystyle \frac{2}{29} $ $ \displaystyle \frac{3}{29} $ $ \displaystyle \frac{4}{29} $ …)の4コ目の分数が200番目の分数で、その数は$ \displaystyle \frac{4}{29} $。(答え) $ \displaystyle \frac{4}{29} $
(3)
(2)の結果を利用する。
第1群の和・・・1
第2群の和・・・2
第3群の和・・・3
第4群の和・・・4
…
第14群の和・・・14
第15群の和・・・$ \displaystyle \frac{1}{29} $+$ \displaystyle \frac{2}{29} $+$ \displaystyle \frac{3}{29} $+$ \displaystyle \frac{4}{29} $=$ \displaystyle \frac{10}{29} $1番目から200番目までの分数をすべて足すと、
1+2+3+…+14+$ \displaystyle \frac{10}{29} $=105$ \displaystyle \frac{10}{29} $(答え) 105$ \displaystyle \frac{10}{29} $