問題
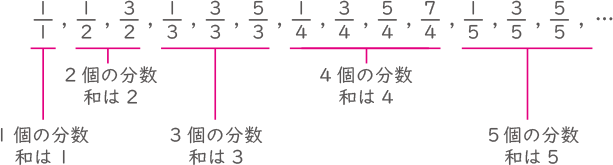
次のように,ある規則にしたがって数が並んでいます。
$ \displaystyle \frac{1}{1} $,$ \displaystyle \frac{1}{2} $,$ \displaystyle \frac{3}{2} $,$ \displaystyle \frac{1}{3} $,$ \displaystyle \frac{3}{3} $,$ \displaystyle \frac{5}{3} $,$ \displaystyle \frac{1}{4} $,$ \displaystyle \frac{3}{4} $,$ \displaystyle \frac{5}{4} $,$ \displaystyle \frac{7}{4} $,$ \displaystyle \frac{1}{5} $,$ \displaystyle \frac{3}{5} $,$ \displaystyle \frac{5}{5} $,…
このとき,次の問いに答えなさい。
(1) $ \displaystyle \frac{7}{11} $が出てくるのは,先頭から数えて何番目ですか。
(2) 先頭から数えて50番目までの和を求めなさい。
Amazonブランドのタブレット[Fire HD 10 Plus タブレット10.1インチ]フルHDディスプレイ(1920×1200)だから広くて見やすく家勉の必需品。
解答
- 解答を開く
-
次のように,ある規則にしたがって数が並んでいます。
$ \displaystyle \frac{1}{1} $,$ \displaystyle \frac{1}{2} $,$ \displaystyle \frac{3}{2} $,$ \displaystyle \frac{1}{3} $,$ \displaystyle \frac{3}{3} $,$ \displaystyle \frac{5}{3} $,$ \displaystyle \frac{1}{4} $,$ \displaystyle \frac{3}{4} $,$ \displaystyle \frac{5}{4} $,$ \displaystyle \frac{7}{4} $,$ \displaystyle \frac{1}{5} $,$ \displaystyle \frac{3}{5} $,$ \displaystyle \frac{5}{5} $,…
このとき,次の問いに答えなさい。
(1) $ \displaystyle \frac{7}{11} $が出てくるのは,先頭から数えて何番目ですか。
(2) 先頭から数えて50番目までの和を求めなさい。(1)
分母が1の分数は1個、分母が2の分数は2個、分母が3の分数は3個、・・・の特徴があり、分子は奇数だけで1から順番に増えてゆく。これをグループで考える。
$ \displaystyle \frac{7}{11} $が出てくるのは11番目のグループの4番目で、先頭から数えると
1個+2個+3個+…+10個+4(11番目のグループの4番目)=59で、59番目。(答え) 59番目
(2)
分母が1の分数は1個で、和は1
分母が2の分数は2個で、和は2
分母が3の分数は3個で、和は3
分母が4の分数は4個で、和は4
…
分母が9の分数は9個で、和は9
ここまでで45個。
残りは5個でその分数は、$ \displaystyle \frac{1}{10} $,$ \displaystyle \frac{3}{10} $,$ \displaystyle \frac{5}{10} $,$ \displaystyle \frac{7}{10} $,$ \displaystyle \frac{9}{10} $
先頭から数えて50番目までの和は、
1+2+3+4+…+9+$ \displaystyle \frac{1}{10} $+$ \displaystyle \frac{3}{10} $+$ \displaystyle \frac{5}{10} $+$ \displaystyle \frac{7}{10} $+$ \displaystyle \frac{9}{10} $=45+$ \displaystyle \frac{25}{10} $=47.5(答え) 47.5