問題
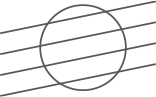
円に直線を1本引くと,図1のように円を2つの部分に分けることができます。
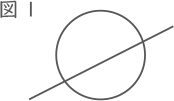
このとき,分けた部分の数を「P=2」と表します。
また,円に直線を2本引くと,図2,図3のように円を3つまたは4つの部分に分けることができます。

このとき,図2は「P=3」,図3は「P=4」となります。
さらに,円に直線を3本引くと,下の図のように円をいくつかの部分に分けることができます。
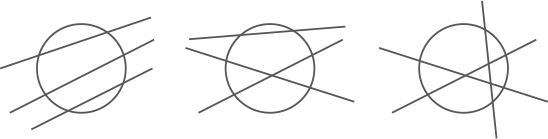
このように,円に直線を何本か引いて,円をいくつかの部分に分けることを考えます。
ただし,下の図のように,2本が円周上で交わったり,3本以上の直線が円の中で1点で交わるような引き方はしないことにします。
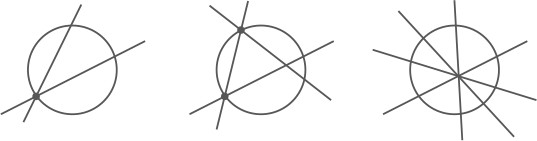
(1) 直線を4本引きます。このとき,最も小さいPを答えなさい。
(2) 直線を7本引きます。このとき,最も大きいPを答えなさい。
(3) 直線を10本引いて円をいくつかの部分に分けます。このとき,最も大きいPと最も小さいPの差を答えなさい。
(4) 直線を何本か引いて,P=106の場合を考えます。このとき直線が最も多い場合は[ ア ]本で,最も少ない場合は[ イ ]本です。[ ア ],[ イ ]にあてはまる数を答えなさい。
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適! 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
円に直線を1本引くと,図1のように円を2つの部分に分けることができます。

このとき,分けた部分の数を「P=2」と表します。
また,円に直線を2本引くと,図2,図3のように円を3つまたは4つの部分に分けることができます。
このとき,図2は「P=3」,図3は「P=4」となります。
さらに,円に直線を3本引くと,下の図のように円をいくつかの部分に分けることができます。
このように,円に直線を何本か引いて,円をいくつかの部分に分けることを考えます。
ただし,下の図のように,2本が円周上で交わったり,3本以上の直線が円の中で1点で交わるような引き方はしないことにします。
(1) 直線を4本引きます。このとき,最も小さいPを答えなさい。
(2) 直線を7本引きます。このとき,最も大きいPを答えなさい。
(3) 直線を10本引いて円をいくつかの部分に分けます。このとき,最も大きいPと最も小さいPの差を答えなさい。
(4) 直線を何本か引いて,P=106の場合を考えます。このとき直線が最も多い場合は[ ア ]本で,最も少ない場合は[ イ ]本です。[ ア ],[ イ ]にあてはまる数を答えなさい。(1)
図2,図3のように、直線が交差しない方が分ける数が少なくなるのでP=5
(答え) 5
(2)
直線を1本引いたとき、Pは2、
直線を2本引いたとき、どの直線も他の直線との交点は1で、最も大きいPは4、
直線を3本引いたとき、どの直線も他の直線との交点は2で、最も大きいPは7、
直線を4本引いたとき、どの直線も他の直線との交点は3で、最も大きいPは11、
直線を5本引いたとき、どの直線も他の直線との交点は4で、最も大きいPは16、
直線を6本引いたとき、どの直線も他の直線との交点は5で、最も大きいPは22、
直線を7本引いたとき、どの直線も他の直線との交点は6で、最も大きいPは29(答え) 29
(3)
(2)より、最も大きいPの数列は、
直線が1本:1+1=2
直線を2本:1+1+2=4
直線を3本:1+1+2+3=7
直線を4本:1+1+2+3+4=11
直線を5本:1+1+2+3+4+5=16
直線を6本:1+1+2+3+4+5+6=22
直線を7本:1+1+2+3+4+5+6+7=29
規則性より、
最も大きいPは1+1+2+3+・・・+10=56で、
最も小さいPは10+1=11、
Pの差は56-11=45(答え) 45
(4)
直線が最も多い場合は106-1=105、
直線が最も少ない場合は、
1+1+2+3+・・・+□=106となる□は、
1+(□+1)×□÷2=106
(□+1)×□=210
□=14(答え) ア 105 イ 14