問題
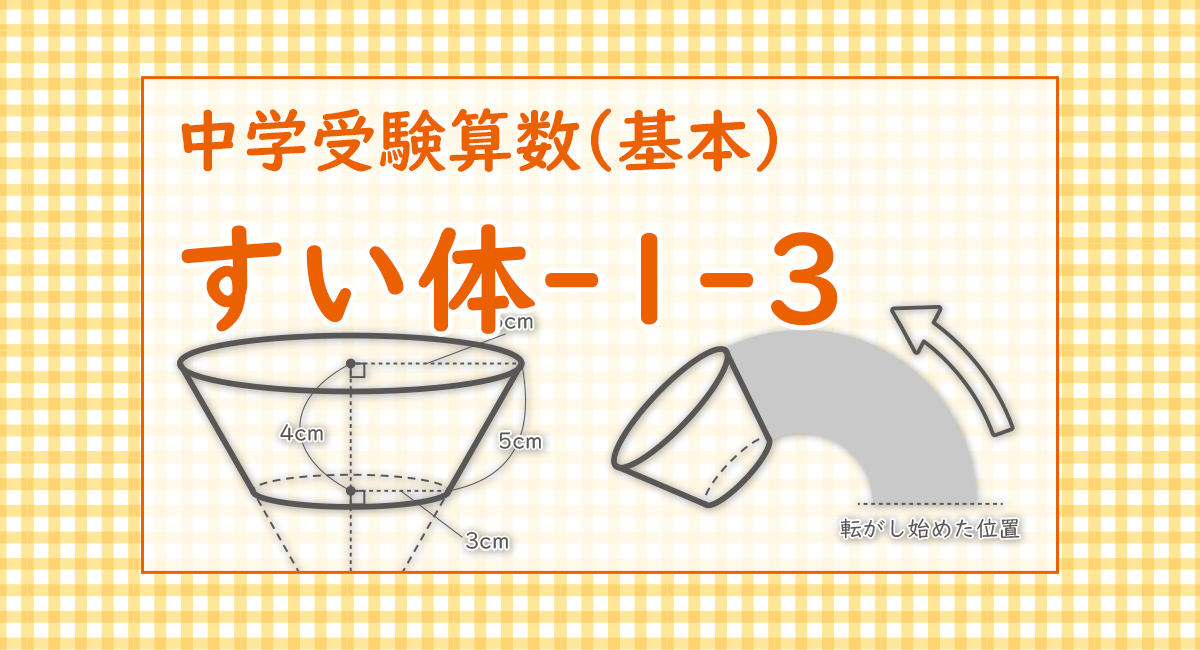
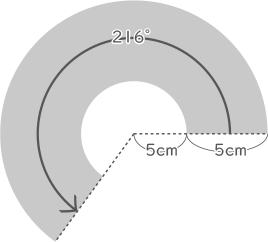
図1のように円すいの一部を切リ取った立体があリます。
この立体の側面にペンキを塗リ,立体を図2のように床に転がして色を付けます。
ただし, 円周率は3.14とします。
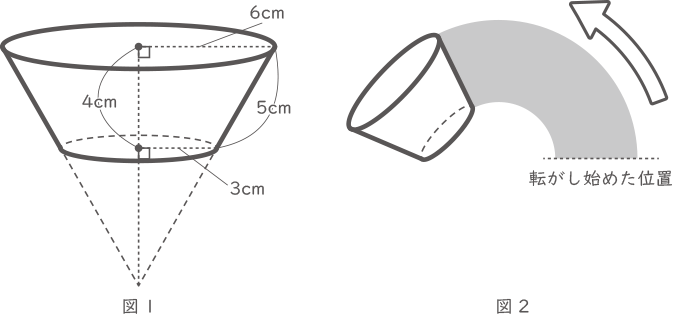
(1) 立体がちょうど1周して転がし始めた位置に戻ったとき,立体は何回転しましたか。
(2) 立体がちょうど1回転したとき,床についたペンキの部分の面積は何cm2ですか。
これまでほとんどの通信教育で実現できなかった難関国私立中学合格。Z会なら、可能です。【公立中高一貫校を受検予定 】の方は試しに資料請求してみましょう。HPにも「小学生コース専科 公立中高一貫校受検対策講座のご案内」が詳しく記載されています。
解答
- 解答を開く
-
図1のように円すいの一部を切リ取った立体があリます。
この立体の側面にペンキを塗リ,立体を図2のように床に転がして色を付けます。
ただし, 円周率は3.14とします。
(1) 立体がちょうど1周して転がし始めた位置に戻ったとき,立体は何回転しましたか。
(2) 立体がちょうど1回転したとき,床についたペンキの部分の面積は何cm2ですか。 (1)
(1)
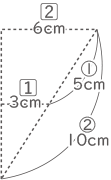
三角すいの中心角は$ \displaystyle \frac{6}{10} $×360°=216°
参照:すい体-1-1(すい体の基本)
$ \displaystyle \frac{360}{216} $=$ \displaystyle \frac{5}{3} $=1$ \displaystyle \frac{2}{3} $(答え) 1$ \displaystyle \frac{2}{3} $回転
 (2)
(2)
(10×10×3.14-5×5×3.14)×$ \displaystyle \frac{216}{360} $
=141.3cm2(答え) 141.3cm2

 (1)
(1) (2)
(2)








