問題
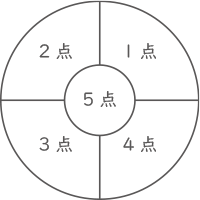
図のような的に矢を3回射って，そのうち高い2回の点数の平均を最終得点とするゲームがあります。J子，G子，K子がこのゲームをしたところ，次のようになりました。
・的を外した人はいませんでした。
・3 回のうち 2回以上同じ点数を取った人はいませんでした。
・K子の1回目の点数は1点でした。
・3人それぞれの最も低い点数は，すべて異なっていました。
・最終得点は，J 子の方がG 子よりも1 点高くなりました。
・3人の最終得点の平均は4点でした。
J子の最終得点は□点，K子の3回の点数は低い方から順に1点，□点，□点でした。
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適！ 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
図のような的に矢を3回射って，そのうち高い2回の点数の平均を最終得点とするゲームがあります。J子，G子，K子がこのゲームをしたところ，次のようになりました。
・的を外した人はいませんでした。
・3 回のうち 2回以上同じ点数を取った人はいませんでした。
・K子の1回目の点数は1点でした。
・3人それぞれの最も低い点数は，すべて異なっていました。
・最終得点は，J 子の方がG 子よりも1 点高くなりました。
・3人の最終得点の平均は4点でした。J子の最終得点は□点，K子の3回の点数は低い方から順に1点，□点，□点でした。
❶ 的を外した人はいませんでした ⇒ 3人は3回とも、なにかしら得点した
❷ 3 回のうち 2回以上同じ点数を取った人はいませんでした ⇒ 3人は3回とも異なる点数であった
❸ K子の1回目の点数は1点でした ⇒ K子の他の点数は2・3・4・5のうちのどれか2つ
❹ 3人それぞれの最も低い点数は，すべて異なっていました ⇒ ❸のことより、J子とG子の最低点はどちらかが2点でもう一人が3点（❷のことより、3回の得点は全て異なり得点の上限は5点）
❺ 最終得点は，J 子の方がG 子よりも1 点高くなりました ⇒ J子は3点・4点・5点であったことが確定する。同時に、G子は2点・3点・4点であったことが確定する。（J子の最終得点は4.5点）
❻ 3人の最終得点の平均は4点でした ⇒ J子（5点・4点）、G子（4点・3点）、K子（△点・□点）。K子の△と□は1点以外なので3点と5点で平均点の4点となる。
（答え） 4.5点 3点 5点
