問題
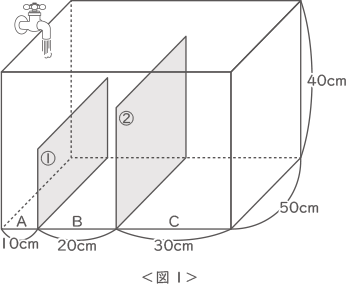
<図1>のような側面に平行な長方形の仕切り①,②で左からA,B,Cの3つの部分に分けられている直方体の水そうがあります。この水そうのAの部分に水を一定の割合で入れていきました。
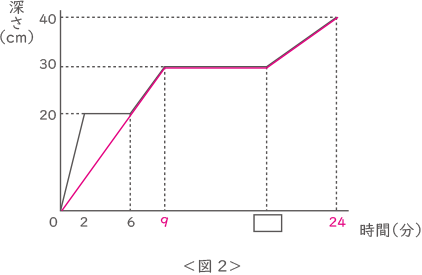
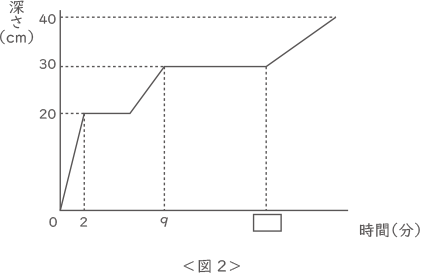
<図2>は,水を入れ始めてからの時間とAの部分の水の深さの関係を表したグラフです。次の問いに答えなさい。ただし,仕切りの厚みは考えないものとします。
(1) 水は毎分何cm3の割合で入っていますか。
(2) グラフの□にあてはまる数を答えなさい。
(3) 水を入れ始める前に仕切り①をとりはずした場合を考えます。仕切り①があった場合と比べて,Aの部分の水の深さが同じになるのは,何分後から何分後ですか。途中の式や考え方も書きなさい。
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適! 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
<図1>のような側面に平行な長方形の仕切り①,②で左からA,B,Cの3つの部分に分けられている直方体の水そうがあります。この水そうのAの部分に水を一定の割合で入れていきました。
<図2>は,水を入れ始めてからの時間とAの部分の水の深さの関係を表したグラフです。次の問いに答えなさい。ただし,仕切りの厚みは考えないものとします。

(1) 水は毎分何cm3の割合で入っていますか。
(2) グラフの□にあてはまる数を答えなさい。
(3) 水を入れ始める前に仕切り①をとりはずした場合を考えます。仕切り①があった場合と比べて,Aの部分の水の深さが同じになるのは,何分後から何分後ですか。途中の式や考え方も書きなさい。(1)
グラフより、2分を過ぎると一定時間深さが20cmのままで変わらない。これは、仕切り①からあふれた水がBに流れている状態。
Aが満たされるまで2分かかり、また、Aの容積は10000cm3(=10×50×20)なので、毎分10000÷2=5000cm3入っている。(答え) 5000cm3
(2)
グラフより、9分を過ぎると一定時間深さが30cmのままで変わらない。これは、仕切り②からあふれた水がCに流れている状態。Cがいっぱいになると、またグラフが上がりだす。
A・B・Cともに仕切り②の高さまで水がたまったときの容量は、(10+20+30)×50×30=9000000cm3で、たるまでの時間が□分。
□=9000000÷5000=18分。(答え) 18分
(3)
仕切り①の高さ20cmを超えて水位があがるときには、仕切り①のありなしは関係なくなる。仕切り①の高さ20cmを超える時間は、
(10+20)×50×20÷5000=6分で、これ以降はグラフは変わらない
40cmの深さまで水がたまる時間は、(10+20+30)×50×40÷5000=24分。
6分後から24分後。
(仕切りが①が無いときのグラフは赤線)
(答え) 6分後から24分後