問題
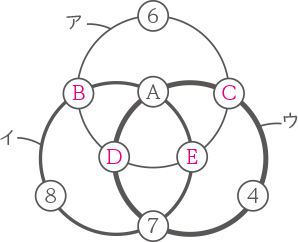
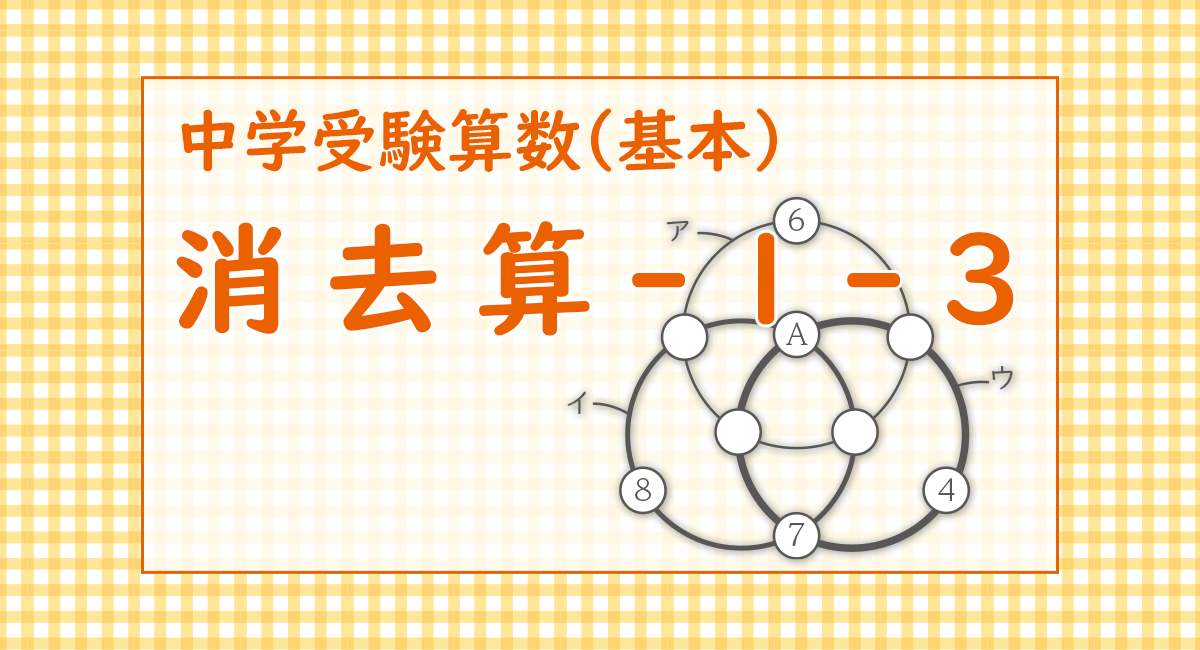
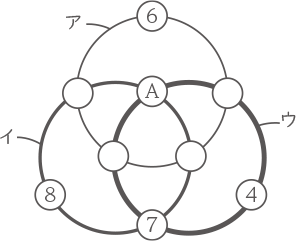右の図のように，3つの円ア，イ，ウがあり，その円周上に9個の白丸があります。この白丸に1から9の異なる整数を一つずつ入れたところ，4,6,7,8は図の位置に入り，アの円周上にある整数の和は23，イの円周上にある整数の和は24，ウの円周上にある整数の和は25になりました。
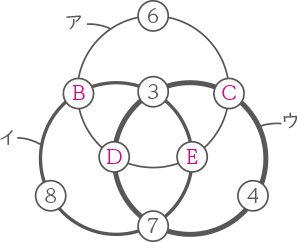
このとき，Aに入った整数は［ ① ］です。次に，この9個の整数のうち2個を選んで入れ替（か）えると，アの円周上にある整数の和は23，イの円周上にある整数の和は21，ウの円周上にある整数の和は28になりました。このとき，入れ替えた整数は［ ② ］と［ ③ ］です。ただし，［ ② ］は［ ③ ］より小さい整数です。
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適！ 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
右の図のように，3つの円ア，イ，ウがあり，その円周上に9個の白丸があります。この白丸に1から9の異なる整数を一つずつ入れたところ，4,6,7,8は図の位置に入り，アの円周上にある整数の和は23，イの円周上にある整数の和は24，ウの円周上にある整数の和は25になりました。このとき，Aに入った整数は［ ① ］です。次に，この9個の整数のうち2個を選んで入れ替（か）えると，アの円周上にある整数の和は23，イの円周上にある整数の和は21，ウの円周上にある整数の和は28になりました。このとき，入れ替えた整数は［ ② ］と［ ③ ］です。ただし，［ ② ］は［ ③ ］より小さい整数です。
空の丸印をB，C，D，Eとする。
アの円周上：23＝B＋C＋D＋E＋6、式を簡単にしてB＋C＋D＋E＝17・・・式１
イの円周上：24＝A＋B＋8＋7＋E、式を簡単にしてA＋B＋E＝9・・・式2
ウの円周上：25＝A＋D＋7＋4＋C、式を簡単にしてA＋D＋C＝14・・・式3
式2と式3の和は、
A＋B＋E＋A＋D＋C＝9＋14
A＋A＋B＋C＋D＋E＝23
式１からB＋C＋D＋Eは17なので、
A＋A＋17＝23
A＝3（①）（答え） ① 3
使われていない整数は1，2，5，9の4つ。また、アの円周上での入れ替えなので、イの円周上とウの円周上に注目する。
入れ替える前
イの円周上：24
ウの円周上：25入れ替えた後
イの円周上：21・・・3減った
ウの円周上：28・・・3増えた3増減するのは2と5の入れ替えのとき。（②と③）
（答え） ② 2 ③ 5
