三角形と四角形-1-3（愛光中学2015/与えられた数字をどのように活用するか）

問題

解答

 解答を開く

 

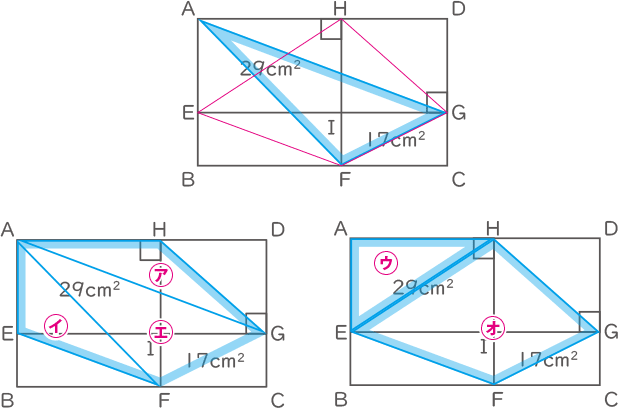
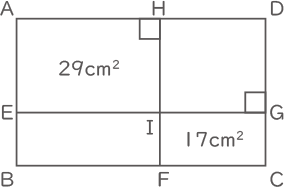右の図のように，EG，HFをひいて長方形ABCDを4つの部分に分けます。四角形AEIHの面積は29cm²で，四角形IFCGの面積は17cm²です。四角形EFGHの面積は三角形AFGの面積より［ ① ］cm²大きく，三角形CHEの面積は三角形AFGの面積より［ ② ］cm²大きいです。

 

---

 

㋐は底辺AHと高さAEより、面積は14.5cm²
㋑は底辺AEと高さAHより、面積は14.5cm²
㋒は底辺AHと高さAEより、面積は14.5cm²
㋓＝五角形AEFGH－㋐－㋑
五角形AEFGH＝㋔＋㋒
よって、㋓＝㋔＋㋒－㋐－㋑
㋓＝㋔＋14.5cm²－14.5cm²－14.5cm²
㋓＝㋔－14.5cm²
㋔四角形EFGHの面積は㋓三角形AFGの面積より14.5cm²大きい。（①）

 

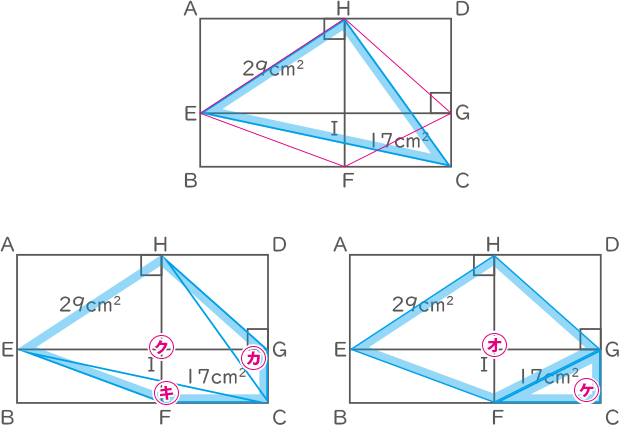
㋖は底辺CFと高さCGより、面積は8.5cm²
㋕は底辺CGと高さCFより、面積は8.5cm²
㋘は底辺CFと高さCGより、面積は8.5cm²
㋗＝五角形CGHEF－㋖－㋕
五角形CGHEF＝㋔＋㋘
よって、㋗＝㋔＋㋘－㋖－㋕
㋗＝㋔＋8.5cm²－8.5cm²－8.5cm²
㋗＝㋔－8.5cm²
これを先程の㋓＝㋔－14.5cm²と比較すると、
㋗三角形CHEの面積は㋓三角形AFGの面積より6cm²（＝14.5－8.5）（②）大きいとわかる。

（答え）　① 14.5　② 6