問題
問題（カリタス女子中学2022/三角形の相似、基本をわかっているか確かめましょう）
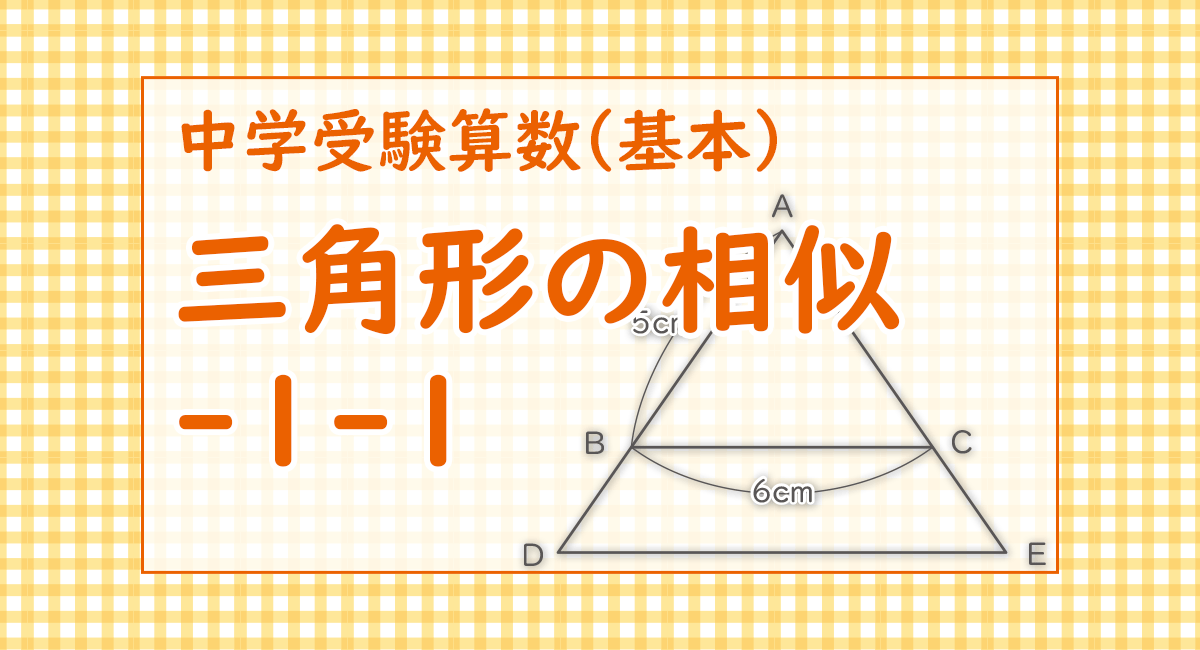
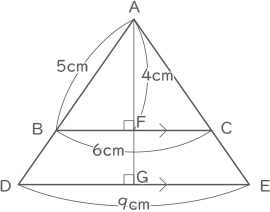
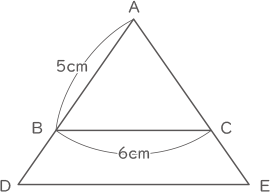右の図の三角形ABCと三角形ADEにおいて、
AB＝5cm，BC＝6cm,
AB：AD＝AC：AE＝2：3
です。このとき、次の問いに答えなさい。
（1） DEの長さは何cmですか。
（2） Aから辺BCに引いた垂線の長さは4cmでした。
（ア）三角形ADEの面積は何cm2ですか。
（イ）四角形BDECの面積は何cm2ですか。
【家庭学習】問題集の画像も大きく見えて小さい文字もきれい
4.35
Amazonブランドのタブレット［Fire HD 10 Plus タブレット10.1インチ］フルHDディスプレイ(1920×1200)だから広くて見やすく家勉の必需品。
解答
- 解答を開く
-
右の図の三角形ABCと三角形ADEにおいて、
AB＝5cm，BC＝6cm,
AB：AD＝AC：AE＝2：3
です。このとき、次の問いに答えなさい。（1） DEの長さは何cmですか。
（2） Aから辺BCに引いた垂線の長さは4cmでした。
（ア）三角形ADEの面積は何cm2ですか。
（イ）四角形BDECの面積は何cm2ですか。AB：AD＝AC：AE → BCとDEは平行
（1）
BC：DE=AB：AD＝2：3
6cm：DE＝2：3
DE＝9cm（答え） 9cm
（2）-（ア）
AF：AG=AB：AD＝2：3
4cm：AG＝2：3
AG＝6cm
よって、三角形ADEの面積＝9×6÷2＝27cm2（答え） 27cm2
（2）-（イ）
FG＝6－4＝2cm
よって、四角形BDECの面積＝（6＋9）×2÷2＝15cm2（答え） 15cm2
（2）-（ア）
ではまた～
