問題
問題(修学旅行の部屋割りを考える・面積図の利用)
修学旅行の部屋割りを担当の先生が考えています。1部屋5人とすると全ての部屋がぴったりうまり、1部屋9人とすると空き部屋が5つと2人の部屋が1つできます。部屋数と生徒数をもとめなさい。
【家庭学習】過去問をA3で実サイズコピーして本番形式で臨みましょう
4.45
試験で使われる問題用紙はかなり大きめ。同じ大きさで過去問を用意して本番感覚を養いましょう。印刷するのはパパとママの役目。A3ノビまで対応、全色顔料インクで滲まない。最大給紙枚数は550枚。
解答
- 解答を開く
-
修学旅行の部屋割りを担当の先生が考えています。1部屋5人とすると全ての部屋がぴったりうまり、1部屋9人とすると空き部屋が5つと2人の部屋が1つできます。部屋数と生徒数をもとめなさい。
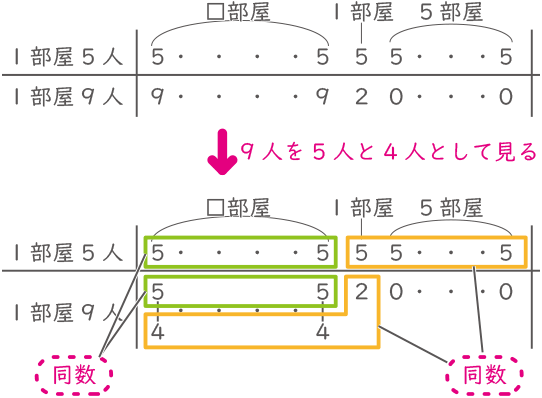
まずは図表を書いてイメージをつかむ。

黄色線は同数となるので4×□+2=5×6、□=7 となり、部屋数=7+1+5=13、生徒数=5×13=65 となる。
(答え)13 部屋、65 人
- 別解を開く
-
修学旅行の部屋割りを担当の先生が考えています。1部屋5人とすると全ての部屋がぴったりうまり、1部屋9人とすると空き部屋が5つと2人の部屋が1つできます。部屋数と生徒数をもとめなさい。
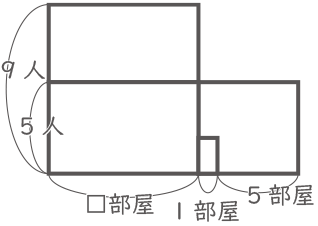
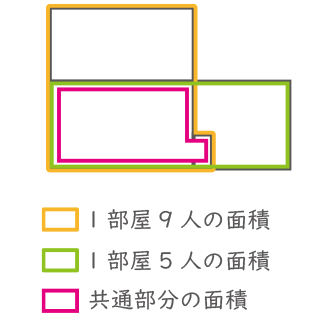
面積図として考える。

9 人で埋まった部屋数を□とし、縦を人数、横を部屋数とする面積図で比べる。

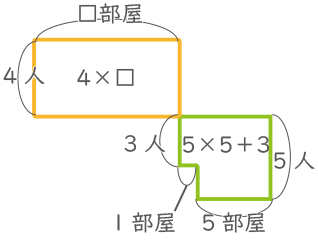
黄色線と緑線は同数になるので、4×□=5×5+3 なので、□=7、よって、部屋数=7+1+5=13、生徒数=5×13=65 となる。
(答え)13 部屋、65 人
ではまた~