問題
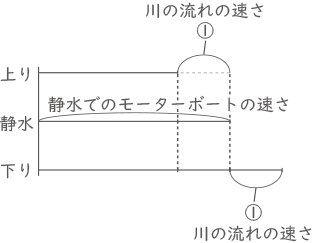
一定の速さで流れる川の下流にA地点が、上流にB地点があります。A地点からモーターボートで川を上ってB地点に行き、またモーターボートで川を下ってA地点に戻(もど)ってくることになりました。
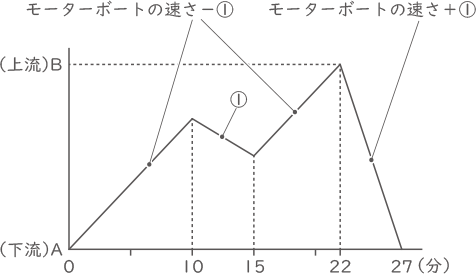
A地点からエンジンをかけてB地点に向かった10分後にエンジンが故障したので、エンジンを切って修理したところ、ボートは川の流れに従いA地点の方に流されました。5分後、修理が終わったので、再びエンジンをかけてB地点に向かったところ、7分でB地点に到着(とうちゃく)しました。帰りは故障もなくA地点に向かったところ、5分でA地点に到着しました。
川の流れの速さは静水時におけるモーターボートの速さの[ ア ]倍であり、エンジンが故障しなければA地点からB地点まで[ イ ]分で到着できます。ただし、静水時におけるモーターボートの速さは一定であるとします。
人里離れた旅館?それとも海辺のリゾートホテル? 中学受験の前に一区切り、受験前最後の家族旅行はお早めに。今がそのチャンスかも。
解答
- 解答を開く
-
一定の速さで流れる川の下流にA地点が、上流にB地点があります。A地点からモーターボートで川を上ってB地点に行き、またモーターボートで川を下ってA地点に戻(もど)ってくることになりました。
A地点からエンジンをかけてB地点に向かった10分後にエンジンが故障したので、エンジンを切って修理したところ、ボートは川の流れに従いA地点の方に流されました。5分後、修理が終わったので、再びエンジンをかけてB地点に向かったところ、7分でB地点に到着(とうちゃく)しました。帰りは故障もなくA地点に向かったところ、5分でA地点に到着しました。
川の流れの速さは静水時におけるモーターボートの速さの[ ア ]倍であり、エンジンが故障しなければA地点からB地点まで[ イ ]分で到着できます。ただし、静水時におけるモーターボートの速さは一定であるとします。
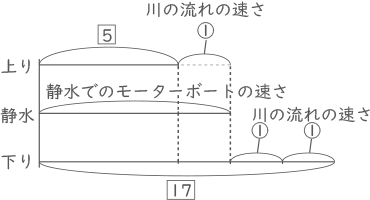
川の流れの速さを①とする。

モーターボートの往復をグラフにする。

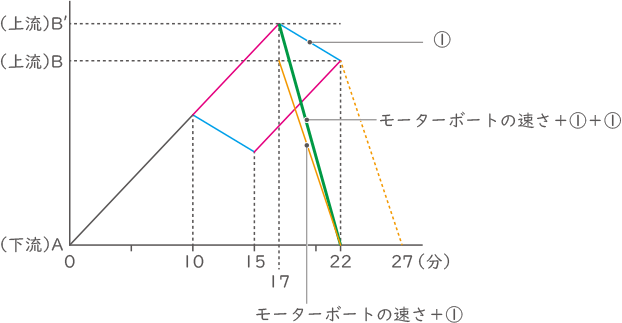
赤線、青線、黄線を平行につくる。青線(川の流れの速さ)と黄線(下りのときの速さ)の和は緑線(下りのとき川の流れの速さが2倍になったとき)となる。

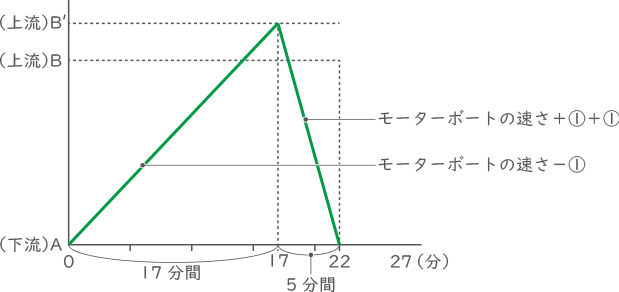
下流Aと上流B′の往復としてグラフをつくる。

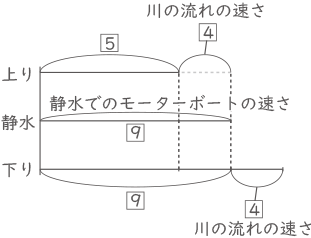
上りは17分間、下りは5分間かかるので、速さの比は逆比となり、上りの速さ:下りの速さ=$ \fbox{5} $: $ \fbox{17} $ 、$ \fbox{17} $-$ \fbox{5} $=$ \fbox{12} $=③、①=$ \fbox{4} $となる。

モーターボートの速さ=$ \fbox{5} $+①=$ \fbox{5} $+$ \fbox{4} $=$ \fbox{9} $
川の流れの速さは$ \fbox{4} $
川の流れの速さは静水時におけるモーターボートの速さの$ \displaystyle \frac{\fbox{4}}{\fbox{9}} $=$ \displaystyle \frac{4}{9} $倍・・・ア川の流れの速さ:静水時におけるモーターボートの速さ=$ \fbox{4} $:$ \fbox{9} $

上りのモーターボートの速さ:下りのモーターボートの速さ= 5 : 13なので、かかる時間は逆比となり、上りの時間:下りの時間=13:5。
下りが5分なので、上りは13分。・・・イ(答え) ア$ \displaystyle \frac{4}{9} $ , イ 13