問題
川の流れの速さが変わると2つの船の出会う地点が変わることについて説明している下記の文の(ア)~(ク)をうめなさい。
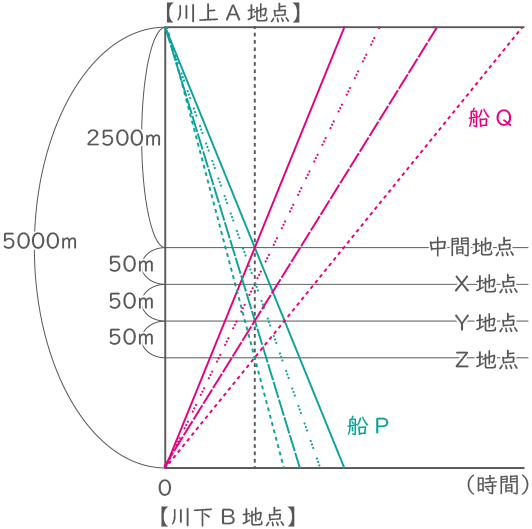
川上のA地点と川下のB地点は5000m離れていて、A地点からB地点に向かって船Pが、B地点からA地点に向かって船Qが同時に動き出します。静水での速さは船P・船Qともに分速500mです。
まず、川の流れの速さが分速10mの場合、2つの船は(ア)分後に中間地点から(イ)mほどB地点よりのところで出会います。ここをX地点とします。
次に、川の流れの速さが分速20mの場合、2つの船は(ウ)分後に中間地点から(エ)mほどB地点よりのところで出会います。ここをY地点とします。
さらに、川の流れの速さが分速30mの場合、2つの船は(オ)分後に中間地点から(カ)mほどB地点よりのところで出会います。ここをZ地点とします。
以上の事より、2つの船の出会う時間は川の流れの速さによらない事が分かりました。
また、川の流れの速さが分速10mから2倍の分速20mになると、出会う地点がX地点から(キ)mずれたY地点になり、川の流れの速さが分速10mから3倍の分速30mになると、出会う地点がX地点から(ク)mずれたZ地点になります。
つまり、川の流れの速さが変わると、【はじめの川の流れの速さと、変わった川の流れの速さの差×分(出会うまでの時間)】だけ、はじめの出会う地点から、出会う位置がずれるという事です。
人里離れた旅館?それとも海辺のリゾートホテル? 中学受験の前に一区切り、受験前最後の家族旅行はお早めに。今がそのチャンスかも。
解答
- 解答を開く
-
川の流れの速さが変わると2つの船の出会う地点が変わることについて説明している下記の文の(ア)~(ク)をうめなさい。
川上のA地点と川下のB地点は5000m離れていて、A地点からB地点に向かって船Pが、B地点からA地点に向かって船Qが同時に動き出します。静水での速さは船P・船Qともに分速500mです。
まず、川の流れの速さが分速10mの場合、2つの船は(ア)分後に中間地点から(イ)mほどB地点よりのところで出会います。ここをX地点とします。
次に、川の流れの速さが分速20mの場合、2つの船は(ウ)分後に中間地点から(エ)mほどB地点よりのところで出会います。ここをY地点とします。
さらに、川の流れの速さが分速30mの場合、2つの船は(オ)分後に中間地点から(カ)mほどB地点よりのところで出会います。ここをZ地点とします。
以上の事より、2つの船の出会う時間は川の流れの速さによらない事が分かりました。
また、川の流れの速さが分速10mから2倍の分速20mになると、出会う地点がX地点から(キ)mずれたY地点になり、川の流れの速さが分速10mから3倍の分速30mになると、出会う地点がX地点から(ク)mずれたZ地点になります。
つまり、川の流れの速さが変わると、【はじめの川の流れの速さと、変わった川の流れの速さの差×分(出会うまでの時間)】だけ、はじめの出会う地点から、出会う位置がずれるという事です。

【川の流れの速さが分速10mの場合】
船Pの速さ:分速500m(静水での船の速さ)+分速10m(流れの速さ)=分速510m
船Qの速さ:分速500m(静水での船の速さ)-分速10m(流れの速さ)=分速490m
2つの船が出会う時間:5000÷(510+490)=5分後・・・(ア)
船Pの進んだ距離:510×5=2550m
中間地点からの距離:2550-2500=50m・・・(イ)【川の流れの速さが分速20mの場合】
船Pの速さ:分速500m(静水での船の速さ)+分速20m(流れの速さ)=分速520m
船Qの速さ:分速500m(静水での船の速さ)-分速20m(流れの速さ)=分速480m
2つの船が出会う時間:5000÷(520+480)=5分後・・・(ウ)
船Pの進んだ距離:520×5=2600m
中間地点からの距離:2600-2500=100m・・・(エ)【川の流れの速さが分速30mの場合】
船Pの速さ:分速500m(静水での船の速さ)+分速30m(流れの速さ)=分速530m
船Qの速さ:分速500m(静水での船の速さ)-分速30m(流れの速さ)=分速470m
2つの船が出会う時間:5000÷(530+470)=5分後・・・(オ)
船Pの進んだ距離:530×5=2650m
中間地点からの距離:2650-2500=150m・・・(カ)X地点は中間地点から2550-2500=50mずれている。
Y地点は中間地点から2600-2500=100mずれている。
Z地点は中間地点から2650-2500=150mずれている。
100m-50m=50m・・・(キ)
150m-50m=100m・・・(ク)(答え)(ア)5 (イ)50 (ウ)5 (エ)100 (オ)5 (カ)150 (キ)50 (ク)100
ポイント川の流れの速さが変わると、【はじめの川の流れの速さと、変わった川の流れの速さの差×分(出会うまでの時間)】だけ、はじめの出会う地点から、出会う位置がずれる