問題
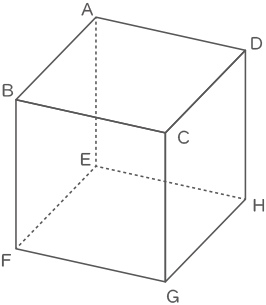
立方体ABCD-EFGHにおいて
正方形ABCDの対角線ACを三等分する点をAに近い方から点P,Q
正方形FGCBの対角線FCを三等分する点をFに近い方から点R,S
正方形HDCGの対角線HCを三等分する点をHに近い方から点T,U
とします。次の各問いに答えなさい。
ただし,角すいの体積は,(底面積)×(高さ)÷3で求められるものとします。
 (1)
(1)
立方体を3点P,R,Tを通る平面で切断したときにできる切り口の図形を(ア),3点Q,S,Uを通る平面で切断したときにできる切り口の図形を(イ)とします。(ア)の面積と(イ)の面積の比を,最も簡単な整数の比で答えなさい。
(2)
立方体を3点P,R,Tを通る平面と,3点Q,R,Tを通る平面で同時に切断したときにできる立体のうち,点Bを含む立体と点Eを含む立体の体積の比を最も簡単な整数の比で答えなさい。
試験で使われる問題用紙はかなり大きめ。同じ大きさで過去問を用意して本番感覚を養いましょう。印刷するのはパパとママの役目。A3ノビまで対応、全色顔料インクで滲まない。最大給紙枚数は550枚。
解答
- 解答を開く
-
立方体ABCD-EFGHにおいて
正方形ABCDの対角線ACを三等分する点をAに近い方から点P,Q
正方形FGCBの対角線FCを三等分する点をFに近い方から点R,S
正方形HDCGの対角線HCを三等分する点をHに近い方から点T,U
とします。次の各問いに答えなさい。
ただし,角すいの体積は,(底面積)×(高さ)÷3で求められるものとします。 (1)
(1)
立方体を3点P,R,Tを通る平面で切断したときにできる切り口の図形を(ア),3点Q,S,Uを通る平面で切断したときにできる切り口の図形を(イ)とします。(ア)の面積と(イ)の面積の比を,最も簡単な整数の比で答えなさい。
(2)
立方体を3点P,R,Tを通る平面と,3点Q,R,Tを通る平面で同時に切断したときにできる立体のうち,点Bを含む立体と点Eを含む立体の体積の比を最も簡単な整数の比で答えなさい。【(1)と(2)で点Hを二箇所で使っており不明瞭な解答となっていた箇所を修正しました。】
(1)
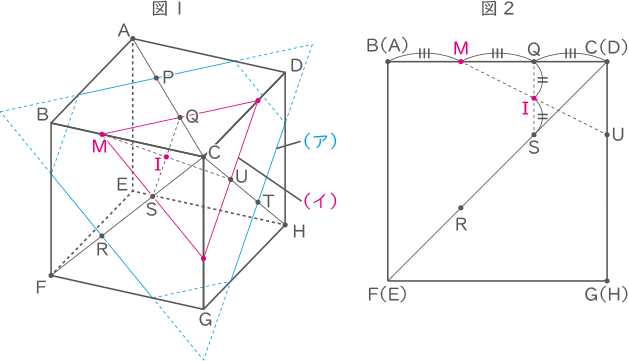
断面(イ)に含まれる点Q,S,Uを使って面の形状を考える。
図2のように、面BCGF側から見たときの位置関係から点M,Iは図1の通り。また、断面(イ)の形状は赤線となる。
断面(ア)に含まれる点P,R,Tを使って面の形状を考える。
図1のように、赤線に平行で点P,R,Tを通る青線をつないで出来る断面が(ア)となる。図1の面MSQの面積を1コ分とすると、(イ)は4コ分、(ア)は13コ分。
(ア)と(イ)の面積比は13:4。
(答え) 13:4
(2)
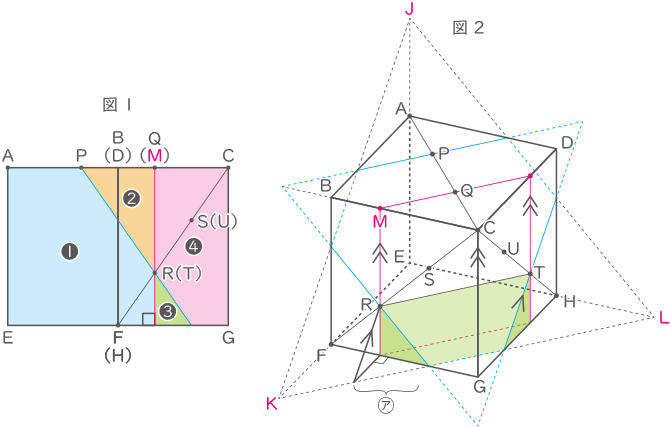
立体を線分BF側から線分DH側に重なる様に見たものが図1で、切断されるそれぞれの立体を❶,❷,❸,❹とする。
最終的に求めるものは<❷の体積:❶の体積>。
図2のように補助線をつくり、線分AB=3として計算する。
(よって、AJ=CM=MR=2,BM=1)
立方体ABCD-EFGHの体積=3×3×3=27
体積(❶+❸)=1×1×$ \displaystyle \frac{1}{2} $×1×$ \displaystyle \frac{1}{3} $×(5×5×5-2×2×2×3)=$ \displaystyle \frac{101}{6} $
体積❸=1×1×$ \displaystyle \frac{1}{2} $×2-1×1×$ \displaystyle \frac{1}{2} $×1×$ \displaystyle \frac{1}{3} $=$ \displaystyle \frac{5}{6} $(三角柱から三角すいの体積㋐をひいている)
体積❹=2×2×$ \displaystyle \frac{1}{2} $×3-$ \displaystyle \frac{5}{6} $=$ \displaystyle \frac{31}{6} $
体積(❷+❹)=27-$ \displaystyle \frac{101}{6} $=$ \displaystyle \frac{61}{6} $体積❶=$ \displaystyle \frac{101}{6} $-$ \displaystyle \frac{5}{6} $=$ \displaystyle \frac{96}{6} $
体積❷=$ \displaystyle \frac{61}{6} $-$ \displaystyle \frac{31}{6} $=$ \displaystyle \frac{30}{6} $❷の体積:❶の体積=$ \displaystyle \frac{30}{6} $:$ \displaystyle \frac{96}{6} $=5:16
(答え) 5:16
大変な問題ですね・・・