問題
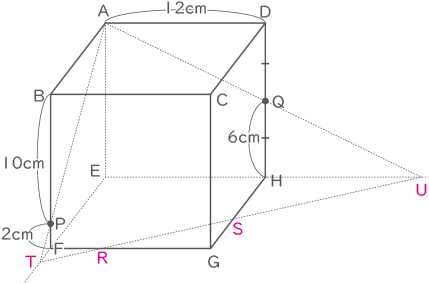
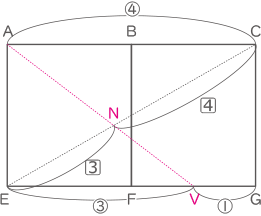
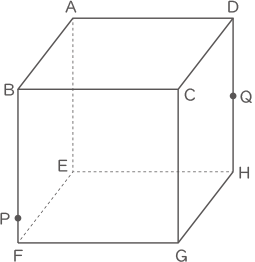
下の図のように,1辺が12cmの立方体ABCD-EFGHがあり,点Pは辺BF上,点Qは辺DH上の点で,BP=10cm,DQ=6cmです。3点A,P,Qを通る平面でこの立方体を切断します。この切断面と辺FG,辺GHが交わる点をそれぞれR,Sとします。次の問いに答えなさい。ただし,角すいの体積は(底面積)×(高さ)÷3で求められるものとします。
(1) FR,SHの長さを求めなさい。
(2) 切断してできた立体のうち,点Eをふくむ方の体積を求めなさい。
(3) 切断面と直線CEが交わる点をNとするとき,CN:NEを最も簡単な整数の比で答えなさい。
人里離れた旅館?それとも海辺のリゾートホテル? 中学受験の前に一区切り、受験前最後の家族旅行はお早めに。今がそのチャンスかも。
解答
- 解答を開く
-
下の図のように,1辺が12cmの立方体ABCD-EFGHがあり,点Pは辺BF上,点Qは辺DH上の点で,BP=10cm,DQ=6cmです。3点A,P,Qを通る平面でこの立方体を切断します。この切断面と辺FG,辺GHが交わる点をそれぞれR,Sとします。次の問いに答えなさい。ただし,角すいの体積は(底面積)×(高さ)÷3で求められるものとします。
(1) FR,SHの長さを求めなさい。
(2) 切断してできた立体のうち,点Eをふくむ方の体積を求めなさい。
(3) 切断面と直線CEが交わる点をNとするとき,CN:NEを最も簡単な整数の比で答えなさい。
(1)
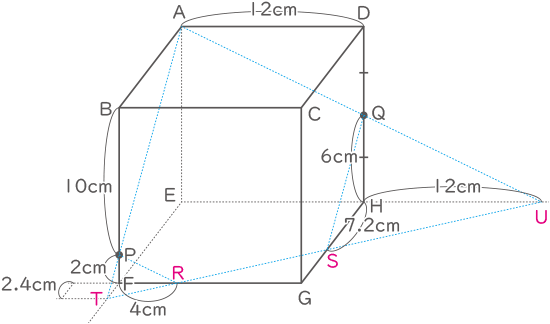
線を延長した交点を点T,Uとする。
三角形PABと三角形PTFは相似なので、AB:BP=TF:FPより、TF=2.4cm
三角形QADと三角形QUHは合同より、HU=12cm
三角形RFTと三角形UETは相似なので、TE:EU=TF:FRより、FR=4cm(答)
三角形UETと三角形UHSは相似なので、TE:EU=SH:HUより、SH=7.2cm(答)(答え) FR=4cm SH=7.2cm
(2)
三角すいA-EUTの体積
(12+12)×(12+2.4)÷2×12÷3=691.2cm3
三角すいP-FRTの体積
4×2.4÷2×2÷3=3.2cm3
三角すいQ-HUSの体積
12×7.2÷2×6÷3=86.4cm3
求める体積=691.2-3.2-86.4=601.6cm3
(答え) 601.6cm3
(3)
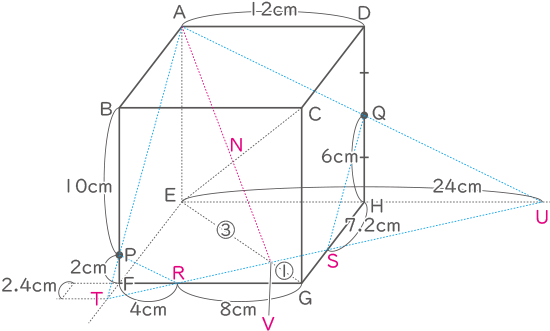
中学受験の範囲ではCEの長さや三角形ATUの面積は求められないので、どこかしら比を見つけるしかなさそう。
着目すべきは、上から見た際のCEとAGが重なって見えるというところ。
EGとRUの交点をVとして、三角形VUEと三角形VRGが相似であることからEV:VG=③:①がわかる。
次にB→D方向に見る。
三角形NCAと三角形NEVが相似であることからCN:NE=4:3とわかる。
(答え) 4:3