問題
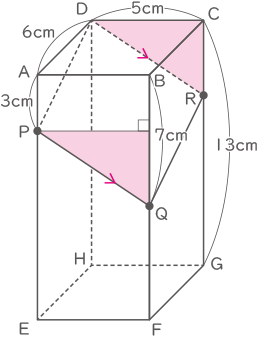
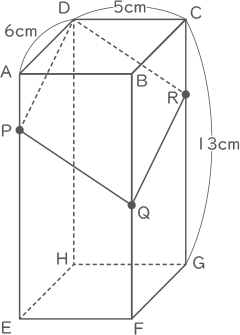 右の図のような縦6cm,横5cm,高さ13cmの直方体があります。辺AE上にAP=3cmとなる点Pをとり、辺BF上にBQ=7cmとなる点Qをとって、3点D,P,Qを通る平面でこの直方体を切り、2つの立体に分けます。次の□に適当な数を入れなさい。
右の図のような縦6cm,横5cm,高さ13cmの直方体があります。辺AE上にAP=3cmとなる点Pをとり、辺BF上にBQ=7cmとなる点Qをとって、3点D,P,Qを通る平面でこの直方体を切り、2つの立体に分けます。次の□に適当な数を入れなさい。
(1) 3点D,P,Qを通る平面が辺CGを切る点をRとするとき、四角形QFGRの面積は□cm2です。
(2) 切り分けられた2つの立体のうち、大きい方の体積は□cm3です。
Amazonブランドのタブレット[Fire HD 10 Plus タブレット10.1インチ]フルHDディスプレイ(1920×1200)だから広くて見やすく家勉の必需品。
解答
- 解答を開く
-
 右の図のような縦6cm,横5cm,高さ13cmの直方体があります。辺AE上にAP=3cmとなる点Pをとり、辺BF上にBQ=7cmとなる点Qをとって、3点D,P,Qを通る平面でこの直方体を切り、2つの立体に分けます。次の□に適当な数を入れなさい。
右の図のような縦6cm,横5cm,高さ13cmの直方体があります。辺AE上にAP=3cmとなる点Pをとり、辺BF上にBQ=7cmとなる点Qをとって、3点D,P,Qを通る平面でこの直方体を切り、2つの立体に分けます。次の□に適当な数を入れなさい。(1) 3点D,P,Qを通る平面が辺CGを切る点をRとするとき、四角形QFGRの面積は□cm2です。
(2) 切り分けられた2つの立体のうち、大きい方の体積は□cm3です。
 (1)
(1)
図の様に、DRとPQは平行なので色の付いた2つの三角形は合同となり、
CR=7-3=4cm
RG=13-4=9cm
よって、□=(6+9)×6÷2=45cm2補足向かい合う高さが等しくなることからもRGの長さを求めることができる。
DH(13)+QF(6)=PE(10)+RGより、
RG=19-10=9cm(答え) 45
(2)
大きい方の立体の上下をひっくり返して重ね合わせれば四角柱ができるので、求める体積はその半分の体積になる。5×6×(13+6(QF))÷2=285cm3
または、
5×6×(10(PE)+9(RG))÷2=285cm3(答え) 285



 (1)
(1)