問題
問題（浅野中学2022/円Xと円Yの一部分が重なってできた図形の各部の面積比）
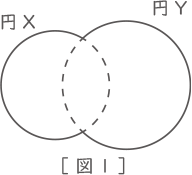［ 図1 ］のように大きさの異なる円Xと円Yの一部分が重なってできた図形があり、全体の面積は143cm2です。重なっている部分の面積は円Xの面積の$ \displaystyle \frac{1}{3} $で、円Yの面積の$ \displaystyle \frac{2}{7} $です。このとき、円Xの面積と円Yの面積の比を、できるだけ簡単な整数の比で答えると［ ア ］：［ イ ］で、円Xの面積は［ ウ ］cm2です。
【家庭学習】問題集の画像も大きく見えて小さい文字もきれい
4.35
Amazonブランドのタブレット［Fire HD 10 Plus タブレット10.1インチ］フルHDディスプレイ(1920×1200)だから広くて見やすく家勉の必需品。
解答
- 解答を開く
-
［ 図1 ］のように大きさの異なる円Xと円Yの一部分が重なってできた図形があり、全体の面積は143cm2です。重なっている部分の面積は円Xの面積の$ \displaystyle \frac{1}{3} $で、円Yの面積の$ \displaystyle \frac{2}{7} $です。このとき、円Xの面積と円Yの面積の比を、できるだけ簡単な整数の比で答えると［ ア ］：［ イ ］で、円Xの面積は［ ウ ］cm2です。
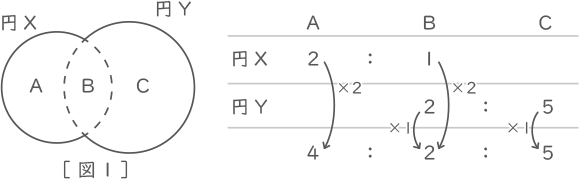
３つの面積をA，B，Cとする。
面積比は、A：B＝2：1で、B：C＝2：5。
Bの数字を合わせるとA：B：C＝④：②：⑤。
よって、円Xの面積：円Yの面積＝（④＋②）：（②＋⑤）=⑥：⑦＝6：7・・・ア，イ全体の面積143cm2＝④＋②＋⑤＝⑪
円Xの面積＝④＋②＝143×$ \displaystyle \frac{⑥}{⑪} $＝78m2（答え） ア 6 ， イ 7 ， ウ 78
ではまた～
