問題
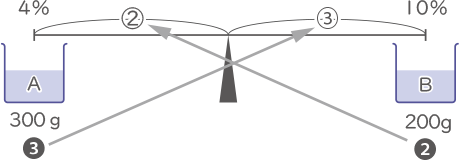
容器Aには濃度4%の食塩水が300g,容器Bには濃度10%の食塩水が200 g入っています。容器Aと容器Bから同じ重さの食塩水を同時に取り出し,容器Aから取り出した食塩水は容器Bに,容器Bから取り出した食塩水は容器Aに入れてよくかき混ぜると,容器Aと容器Bの食塩水の濃度は等しくなりました。
(1) かき混ぜた後の容器Aの食塩水の濃度は何%ですか。
(2) 容器Aから取り出した食塩水の重さは何gですか。
これまでほとんどの通信教育で実現できなかった難関国私立中学合格。Z会なら、可能です。【公立中高一貫校を受検予定 】の方は試しに資料請求してみましょう。HPにも「小学生コース専科 公立中高一貫校受検対策講座のご案内」が詳しく記載されています。
解答
- 解答を開く
-
容器Aには濃度4%の食塩水が300g,容器Bには濃度10%の食塩水が200 g入っています。容器Aと容器Bから同じ重さの食塩水を同時に取り出し,容器Aから取り出した食塩水は容器Bに,容器Bから取り出した食塩水は容器Aに入れてよくかき混ぜると,容器Aと容器Bの食塩水の濃度は等しくなりました。
(1) かき混ぜた後の容器Aの食塩水の濃度は何%ですか。
(2) 容器Aから取り出した食塩水の重さは何gですか。(1)
容器Aと容器Bの食塩水の濃度は等しくなった ⇒ 全て混ぜ合わせても濃度は同じ
4+(10-4)×$ \displaystyle \frac{②}{⑤} $=6.4
(答え) 6.4%
(2)
取り出した食塩水の量を□gとする。
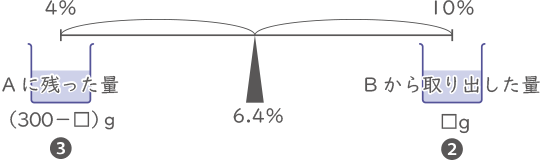
(1)のことより、容器Aの食塩水の重さ:容器Bの食塩水の重さ=3:2となれば濃度が6.4%になる。
(300-□):□=❸:❷となる□を求める。
300-□=❸
□=❷
❶=60
□=120、容器Aから取り出した食塩水の重さ□は120g。(答え) 120g