問題
あるイベント会場の入場ゲートで,受付けを開始しようとしたところ,すでに660人の人が受付けの順番を待っています。その後も毎分10人の割合で人が増えていきます。今までの経験から,入場ゲートの窓口を3つにして受付けを開始すると,ちょうど60分で受付けの順番を待つ人がいなくなることがわかっています。このとき,次の各問いに答えなさい。
(1) 1つの窓口では1分間に何人,受付けができますか。
(2) 窓口を5つにして受付けを開始すると,受付けの順番を待つ人がいなくなるのにかかる時間は何分何秒ですか。
(3) 窓口を5つにして受付けを開始し,途中で窓口をさらに4か所増やしたところ,受付けを開始してからちょうど18分で受付けの順番を待つ人がいなくなりました。最初の5か所の窓口で受付けをしていた時間は何分何秒ですか。
灘をはじめ、名だたる難関中学に毎年多数の合格者を出す「浜学園」。講師の質や、教材のよさは折り紙付き。引きつりそうな料金設定ですが、中学受験をすると決めたら偏差値を買うんだ!ぐらいの前向きな気持ちで行きましょう。気になる方は資料請求してお子さんに合いそうか是非確認してみましょう。もちろん、体験入塾も無料で用意されています。
解答
- 解答を開く
-
あるイベント会場の入場ゲートで,受付けを開始しようとしたところ,すでに660人の人が受付けの順番を待っています。その後も毎分10人の割合で人が増えていきます。今までの経験から,入場ゲートの窓口を3つにして受付けを開始すると,ちょうど60分で受付けの順番を待つ人がいなくなることがわかっています。このとき,次の各問いに答えなさい。
(1) 1つの窓口では1分間に何人,受付けができますか。
(2) 窓口を5つにして受付けを開始すると,受付けの順番を待つ人がいなくなるのにかかる時間は何分何秒ですか。
(3) 窓口を5つにして受付けを開始し,途中で窓口をさらに4か所増やしたところ,受付けを開始してからちょうど18分で受付けの順番を待つ人がいなくなりました。最初の5か所の窓口で受付けをしていた時間は何分何秒ですか。
(1)
1分間に1つの窓口で受付できる人数を$ \fbox{1} $とする。
$ \fbox{180} $が1260人なので$ \fbox{1} $は7人にあたる。
(答え) 7人
(2)
かかる時間を△として線分図の様に考える。
7×5×△=660+10×△
35×△=660+10×△
25×△=660
△=26.4=26$ \displaystyle \frac{4}{10} $=26$ \displaystyle \frac{24}{60} $=26分24秒
(答え) 26分24秒
(3)
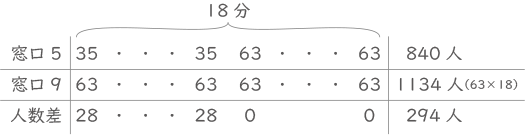
18分で受付した人数は660+10×18=840人。
1分間に、5つの窓口では35人、9つの窓口では63人受付できる。
1分あたり28人の差があり、その合計が294人。
よって、5つの窓口だった時間は294÷28=10.5 10分30秒。(答え) 10分30秒