面積比-3-1（栄東中学-東大クラス選抜1月12日-2022/普段、丁寧な作図作業をしていないと・・・）

1 問題
2 解答

問題

問題（栄東中学-東大クラス選抜1月12日-2022/普段、丁寧な作図作業をしていないと・・・）

栄くんは次の問題に取り組んでいます。

《問題》
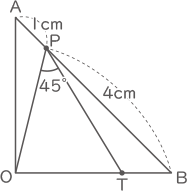
角AOB=90゜，辺AB=5cmの直角二等辺三角形OABの辺AB上にAP=1cm，PB=4cmとなる点Pをとり，辺OB上に角OPT=45゜となる点Tをとります。このときOTとTBの長さの比を求めなさい。

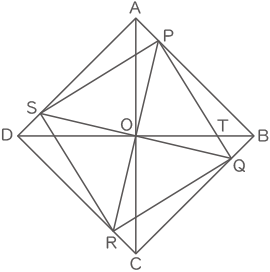栄くんが悩んでいると，東さんが「三角形OABと合同な三角形をあと3つ用意して，敷き詰めてみたらどうかな？」と言って，次の図をかいてくれました。

（1）東さんがかいた図において，三角形OPQの面積を求めなさい。

（2）栄くんが取り組んでいた問題に答えなさい。

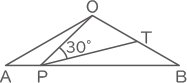（3）角AOB=120゜，辺AB=5cmの二等辺三角形OABの辺 AB上に AP=1cm，PB=4cmとなる点Pをとり，辺OB上に角OPT=30゜となる点Tをとります。このときOTとTBの長さの比をもっとも簡単な整数の比で求めなさい。
《解答欄の考え方を記す欄に考え方も書きなさい》

試験で使われる問題用紙はかなり大きめ。同じ大きさで過去問を用意して本番感覚を養いましょう。印刷するのはパパとママの役目。A3ノビまで対応、全色顔料インクで滲まない。最大給紙枚数は550枚。

解答

解答を開く

栄くんは次の問題に取り組んでいます。

（1）東さんがかいた図において，三角形OPQの面積を求めなさい。

（2）栄くんが取り組んでいた問題に答えなさい。

（1）
図形ABCDと図形PQRSは共に正方形で、三角形OPQは正方形PQRSの$ \displaystyle \frac{1}{4} $。
三角形OPQの面積＝（正方形ABCD－三角形BPQ×4）×$ \displaystyle \frac{1}{4} $
＝（25－1×4×$ \displaystyle \frac{1}{2} $×4）×$ \displaystyle \frac{1}{4} $＝4.25cm²

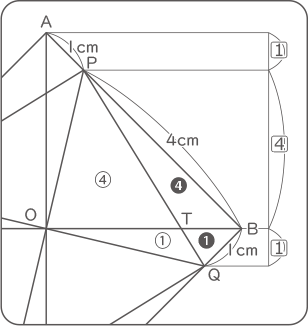
（答え）　4.25cm²

（2）
図の様に高さは$ \fbox{1} $：$ \fbox{4} $：$ \fbox{1} $の比になる。
三角形QBPの面積は2cm²で、底辺をTBと考えると三角形TBP：三角形TBQの面積比は❹：❶、よって、三角形TBPの面積は（2×$ \displaystyle \frac{4}{5} $）＝1.6cm²。
三角形OPQの面積は4.25cm²で、底辺をTOと考えると三角形TOP：三角形TOQの面積比は④：①、よって、三角形TOPの面積は4.25×$ \displaystyle \frac{4}{5} $＝3.4cm²。

三角形TOPと三角形TBPは高さが同じなので底辺の長さOT：TB＝3.4：1.6＝17：8。

（答え）　17：8

（3）
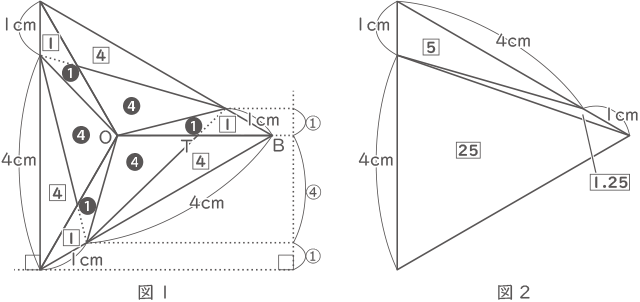
【図1】
東さんの手順と同じように合同な三角形をあと２つ用意し、敷き詰めると、２つの大きさの違う正三角形が出来る。
さらに、高さは①：④：①の比になるので各三角形の面積比は図の様に表すことができる。
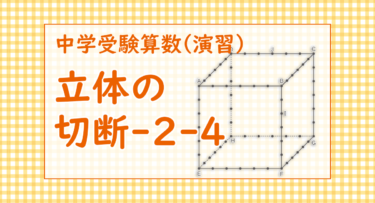
【図2】
白□の面積比だけで表すと大きな正三角形は$ \fbox{5} $＋$ \fbox{25} $＋$ \fbox{1.25} $＝$ \fbox{31.25} $になる。