問題
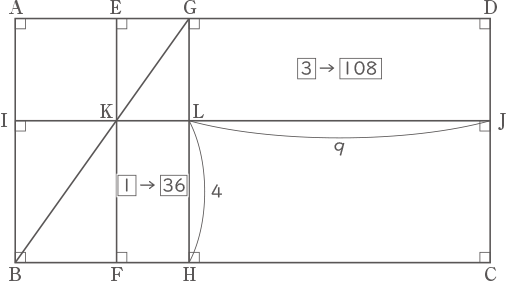
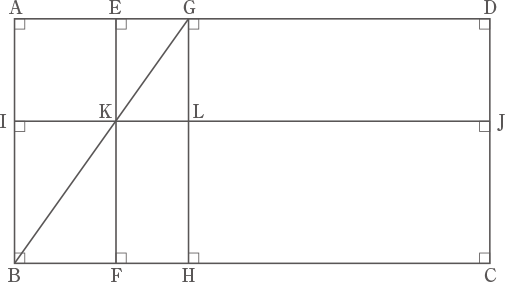
下の図の四角形ABCDは長方形で,EF,GHは長方形の縦の辺に,IJは横の辺にそれぞれ平行です。また,長方形ABHGの対角線BGは,EFとIJの交点Kを通ります。
四角形AIKEが正方形で,長方形KFHLと長方形GLJDの面積の比が1:3,LHとLJの長さの比が4:9です。次の問いに答えなさい。
① 正方形AIKEと長方形KFHLの面積の比を最も簡単な整数の比で答えなさい。
② 正方形AIKEの面積が24cm2のとき,長方形ABCDの面積を答えなさい。
試験で使われる問題用紙はかなり大きめ。同じ大きさで過去問を用意して本番感覚を養いましょう。印刷するのはパパとママの役目。A3ノビまで対応、全色顔料インクで滲まない。最大給紙枚数は550枚。
解答
- 解答を開く
-
下の図の四角形ABCDは長方形で,EF,GHは長方形の縦の辺に,IJは横の辺にそれぞれ平行です。また,長方形ABHGの対角線BGは,EFとIJの交点Kを通ります。
四角形AIKEが正方形で,長方形KFHLと長方形GLJDの面積の比が1:3,LHとLJの長さの比が4:9です。次の問いに答えなさい。
① 正方形AIKEと長方形KFHLの面積の比を最も簡単な整数の比で答えなさい。
② 正方形AIKEの面積が24cm2のとき,長方形ABCDの面積を答えなさい。

長方形KFHLと長方形GLJDの面積比1:3を36(=4×9)倍し、$ \fbox{36} $:$ \fbox{108} $とする。
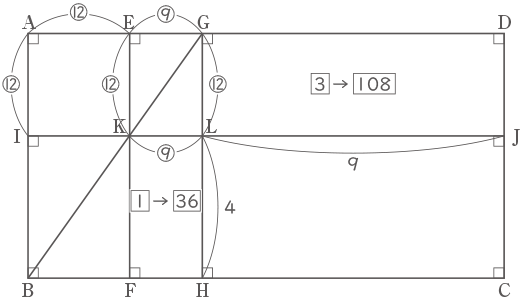
$ \fbox{108} $÷9=12,$ \fbox{36} $÷4=9より、LG:LK=⑫:⑨(④:③でもよいが後の計算が整数になるのでこのままにしておく。)
三角形GEKと三角形GABは相似なので、GE:EK=GA:ABとなる。
⑨:⑫=㉑:AB、AB=㉘、IB=㉘-⑫=⑯=LH
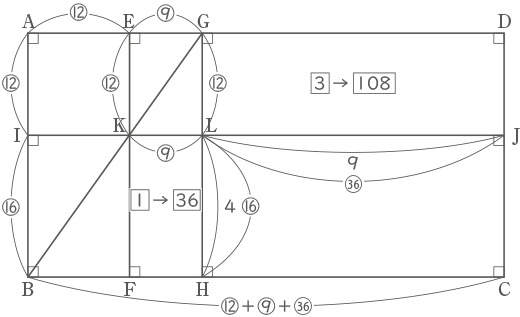
よって、$ \fbox{36} $=⑨×⑯より、$ \fbox{1} $=④、$ \fbox{108} $=⑫×㊱、LJ=㊱とわかる。
正方形AIKEと長方形KFHLの面積=⑫×⑫:⑨×⑯=1:1・・・(①の解答)
正方形AIKEの面積が24m2のとき、⑫×⑫=24m2より、⑥=1m2
長方形ABCDの面積は、(⑫+⑯)×(⑫+⑨+㊱)÷⑥=266m2・・・(②の解答)(答え) ① 1:1 , ② 266m2