問題
問題（鴎友学園女子中学2006/連比を使った面積比の求め方）
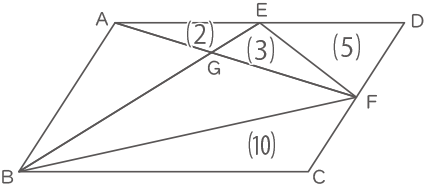
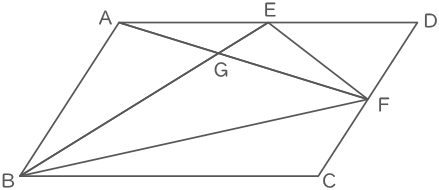
下の図の平行四辺形ABCDでAE＝ED，DF＝FCです。このとき，三角形EFGと三角形BCFの面積の比を，最も簡単な整数の比で表しなさい。
【家庭学習】過去問をA３で実サイズコピーして本番形式で臨みましょう
4.45
試験で使われる問題用紙はかなり大きめ。同じ大きさで過去問を用意して本番感覚を養いましょう。印刷するのはパパとママの役目。A3ノビまで対応、全色顔料インクで滲まない。最大給紙枚数は550枚。
解答
- 解答を開く
-
下の図の平行四辺形ABCDでAE＝ED，DF＝FCです。このとき，三角形EFGと三角形BCFの面積の比を，最も簡単な整数の比で表しなさい。
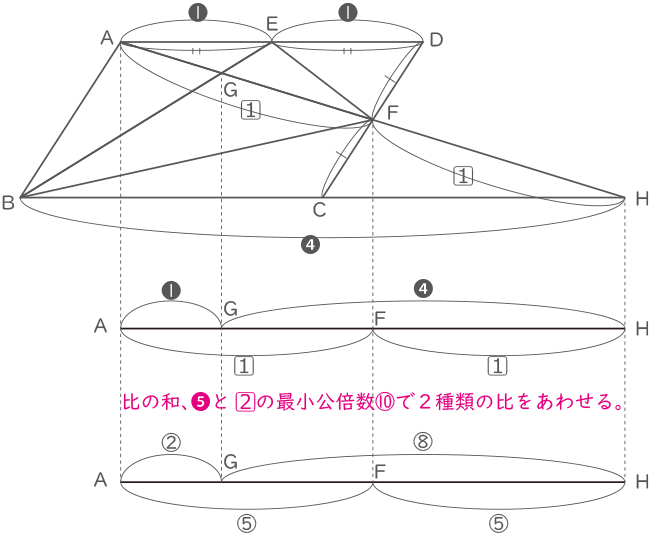
図の様にAFとBCの延長線となる補助線を引き、交点を点Hとする。三角形AGEと三角形HGBが相似となりAG：HG＝1：4とわかる。
2種類の比を、項の和の最小公倍数⑩であわせた連比にするとAG：GF：FH＝②：③：⑤となる。
三角形AGEと三角形FGEは高さが同じことと、AG：FG＝②：③より、面積比は2：3とわかる。
三角形AGEの面積を⑵、三角形EFGの面積を⑶とおくと、三角形AFEの面積は⑸となる。
三角形AFEと三角形DFEはAE＝DEで高さが同じなので、三角形DFEの面積も⑸となる。三角形AFDの面積は⑽となり、三角形BCFも⑽となる。
よって、三角形EFGの面積：三角形BCFの面積＝⑶：⑽。（答え） 3：10
図の様にAFとBCの延長線となる補助線を引き、交点を点Hとする。三角形AGEと三角形HGBが相似となりAG：HG＝1：4とわかる。
ではまた～
