問題
問題(慶應義塾中等部2010/面積比を求める定番問題2)
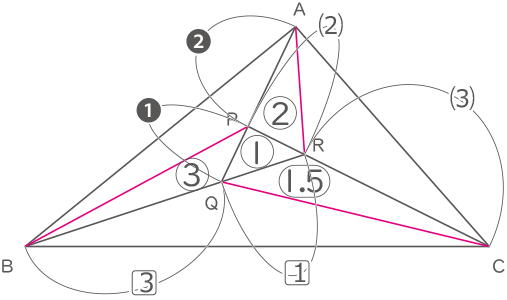
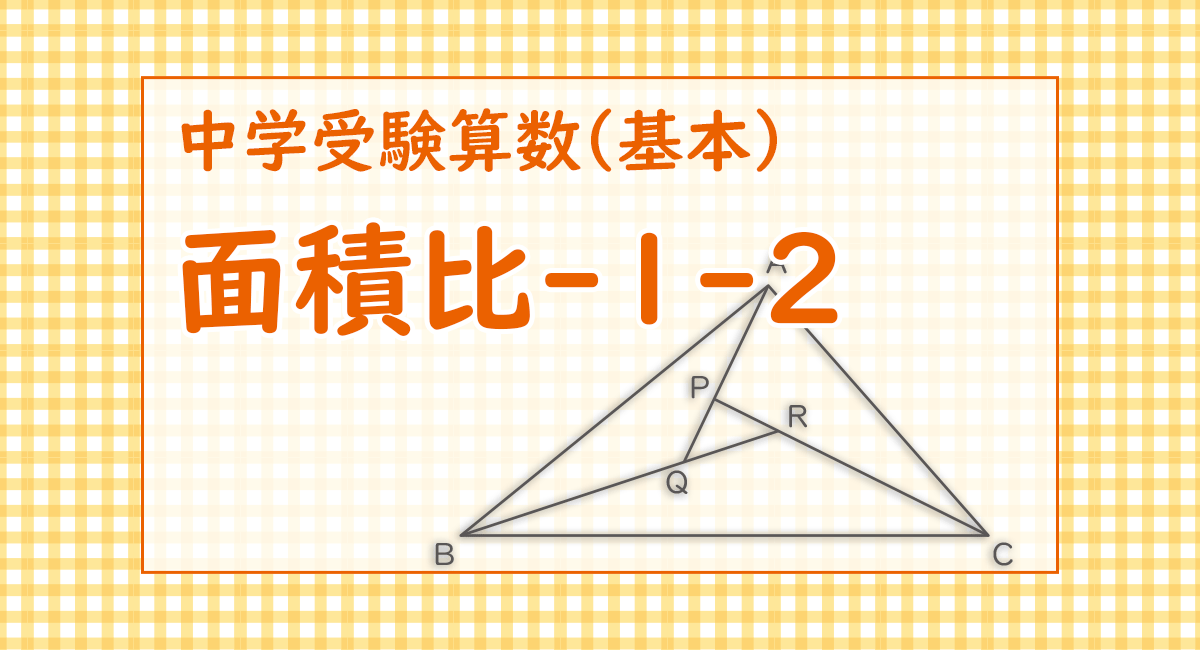
[図2]のように,三角形ABCの中に,それぞれAP:PQ=2:1,BQ:QR=3:1,CR:RP=3:2になるような点P,Q,Rをとります。三角形ABCの面積が441cm2のとき,三角形PQRの面積は,□cm2になります。
関西で一番信頼出来る中学受験塾「浜学園」
4.72
灘をはじめ、名だたる難関中学に毎年多数の合格者を出す「浜学園」。講師の質や、教材のよさは折り紙付き。引きつりそうな料金設定ですが、中学受験をすると決めたら偏差値を買うんだ!ぐらいの前向きな気持ちで行きましょう。気になる方は資料請求してお子さんに合いそうか是非確認してみましょう。もちろん、体験入塾も無料で用意されています。
解答
- 解答を開く
-
[図2]のように,三角形ABCの中に,それぞれAP:PQ=2:1,BQ:QR=3:1,CR:RP=3:2になるような点P,Q,Rをとります。三角形ABCの面積が441cm2のとき,三角形PQRの面積は,□cm2になります。


図の様に補助線を赤線で追加し、三角形PQRの面積を①とおく。
三角形PQRと三角形PRAは高さが同じなので面積比は①:②。
三角形PQRと三角形PQBは高さが同じなので面積比は①:③。
三角形PQRと三角形CRQは高さが同じなので面積比は①:(マル1.5)。
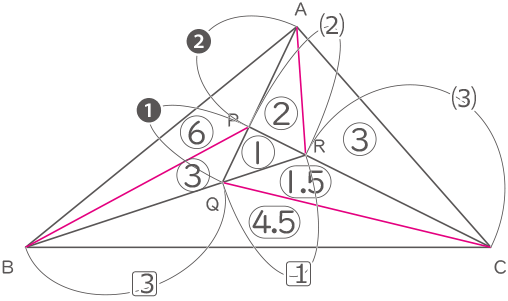
面積が分からない残りの三角形についても比を使って求める。
三角形PRAと三角形CRAは高さが同じなので面積比は②:③。
三角形BQPと三角形BAPは高さが同じなので面積比は③:⑥。
三角形CRQと三角形CBQは高さが同じなので面積比は(マル1.5):(マル4.5)。全ての和は②+⑥+③+①+③+(マル1.5)+(マル4.5)=㉑
㉑が441cm2なので①は441÷21=21cm2(答え) 21
ではまた~