問題
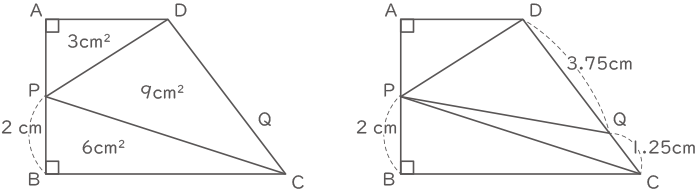
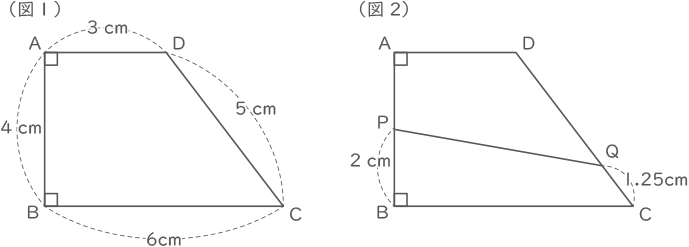
図1のように、辺ADと辺BCが平行であり、AB=4cm、BC=6cm、CD=5cm、DA=3cmである台形ABCDがあります。
(1) 図2のように、点Pを辺AB上でBP=2cmとなるところに、点Qを辺CD上でCQ= 1.25 cmとなるところにとります。このとき、四角形PBCQの面積は何cm2ですか。
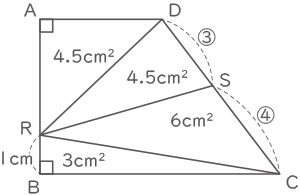
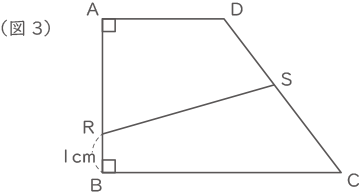
(2) 図3のように、点Rを辺AB上でBR=1cmとなるところにとり、点Sを辺CD上にとったところ、四角形ARSDの面積と四角形RBCSの面積が等しくなりました。このとき、CSとSDの長さの比は何対何ですか。
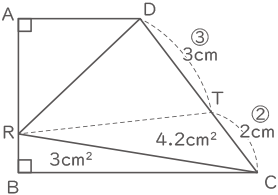
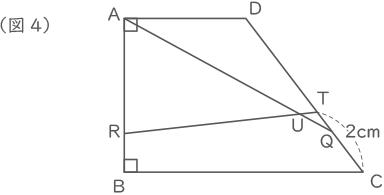
(3) 図4のように、(1)の点Qと(2)の点Rを台形ABCDにとり、さらに点Tを辺CD上でCT=2cmとなるところにとります。点Aと点Qを結ぶ線と、点Rと点Tを結ぶ線が交わる点をUとするとき、五角形RBCQUの面積は何cm2ですか。
人里離れた旅館?それとも海辺のリゾートホテル? 中学受験の前に一区切り、受験前最後の家族旅行はお早めに。今がそのチャンスかも。
解答
- 解答を開く
-
図1のように、辺ADと辺BCが平行であり、AB=4cm、BC=6cm、CD=5cm、DA=3cmである台形ABCDがあります。
(1) 図2のように、点Pを辺AB上でBP=2cmとなるところに、点Qを辺CD上でCQ= 1.25 cmとなるところにとります。このとき、四角形PBCQの面積は何cm2ですか。

(2) 図3のように、点Rを辺AB上でBR=1cmとなるところにとり、点Sを辺CD上にとったところ、四角形ARSDの面積と四角形RBCSの面積が等しくなりました。このとき、CSとSDの長さの比は何対何ですか。

(3) 図4のように、(1)の点Qと(2)の点Rを台形ABCDにとり、さらに点Tを辺CD上でCT=2cmとなるところにとります。点Aと点Qを結ぶ線と、点Rと点Tを結ぶ線が交わる点をUとするとき、五角形RBCQUの面積は何cm2ですか。

(1)
台形ABCDの面積=(3+6)×4÷2=18cm2
三角形ADPの面積=3×2÷2=3cm2
三角形BCPの面積=6×2÷2=6cm2
三角形PCDの面積=18-3-6=9cm2
三角形PCDの辺の比、3.75:1.25=3:1を使うと、三角形PCQの面積=9×$ \displaystyle \frac{1}{4} $=2.25
四角形PBCQの面積=6+2.25=8.25cm2(答え) 8.25cm2
(2)
三角形ADRの面積=3×3÷2=4.5cm2
三角形BCRの面積=6×1÷2=3cm2
三角形CDRの面積=18-4.5-3=10.5cm2
よって、
三角形DRSの面積が18÷2-4.5=4.5cm2になり、
三角形CRSの面積が10.5-4.5=6cm2になればよい。
そのためにはCS:SD=6:4.5=4:3となればよい。
(答え) 4:3
(3)
【四角形RBCTの面積を求める】
(2)より、三角形CDRの面積=10.5cm2
DT:TC=3:2より、三角形CTRの面積=三角形CDRの面積×$ \displaystyle \frac{2}{5} $=4.2cm2
四角形RBCTの面積=4.2+1×6÷2=7.2cm2
この面積から三角形QUTの面積を引いて五角形RBCQUの面積を求める。
【三角形QUTの面積を求める】
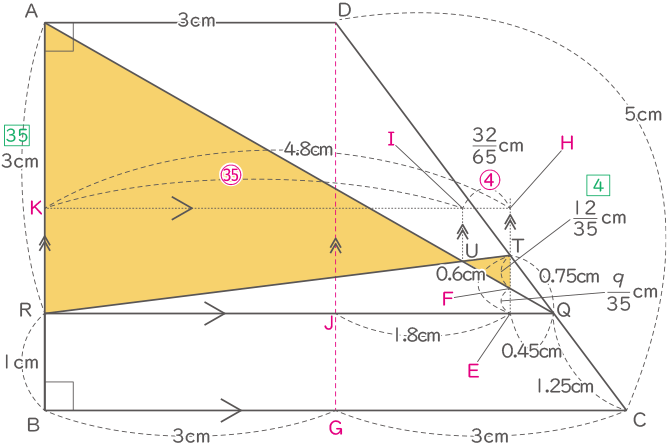
下図のようにE,F,G,H,I,J,Kの点と補助線を追記する。
(計算は省くが)RQとBCは平行になる。(1.25という数字には意味があったようだ。)
DG:GC=DJ:JQより、JQ=2.25cm、
DG:GC:CD=TE:EQ:QTより、TE=0.6cm、EQ=0.45cm、関連してJE=1.8cm
AR:RQ=FE:EQより、FE=$ \displaystyle \frac{9}{35} $cm、さらにTF=$ \displaystyle \frac{12}{35} $cm
(これで相似な三角形の相似比が求められるようになった。)
黄色の三角形ARUと三角形FTUは相似なので、AR:FT=KI:HI=㉟:④
KH=BG+JE=4.8cm
HI=4.8×$ \displaystyle \frac{④}{㉟+④} $=$ \displaystyle \frac{32}{65} $cm
三角形QUTの面積=三角形TFU+三角形TFQ
=$ \displaystyle \frac{12}{35} $×($ \displaystyle \frac{32}{65} $+0.45)×$ \displaystyle \frac{1}{2} $=$ \displaystyle \frac{21}{130} $cm2求める面積=四角形RBCTの面積-三角形QUTの面積=7.2-$ \displaystyle \frac{21}{130} $=7$ \displaystyle \frac{1}{26} $cm2
(答え) 7$ \displaystyle \frac{1}{26} $cm2
補足三角形QUTが小さいのでどうしても外側に補助線を引こうと考えてしまう。三角形の相似が見つかっても途中の計算量が多く正確な数字で最後までたどり着けるか、配点の割に大量の時間を消費することも不安。この手の問題は勇気をもって飛ばしてしまいましょう。