問題
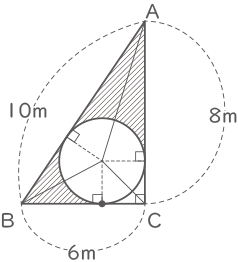
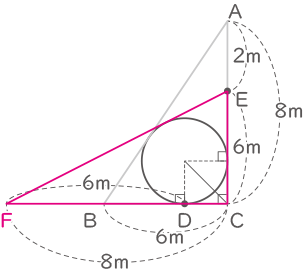
下の図は、AB=10m,BC=6m,CA=8m,角Cが90°の直角三角形です。また、円と辺AB,BC,CAにすきまはないものとします。次の問いに答えなさい。(円周率は3.14)
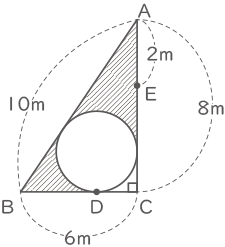
(1) 三角形ABCの面積を利用して円の半径を求めなさい。
(2) 斜線部分の面積の合計を求めなさい。
(3) 三角形ABCの斜線部分以外をAとCを通る直線を軸にして回転させた。えられる立体は点Dが回転する平面に置かれているとします。以下、この平面を地面とします。立体に点Aから光を当てたとき、地面(立体のある部分以外)にできる影の面積を求めなさい。
(4) (3)の立体に点Aの2m下の点Eから光を当てたとき、地面(立体のある部分以外)にできる影の面積は(3)の面積の何倍になるのかを求めなさい。
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適! 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
下の図は、AB=10m,BC=6m,CA=8m,角Cが90°の直角三角形です。また、円と辺AB,BC,CAにすきまはないものとします。次の問いに答えなさい。(円周率は3.14)

(1) 三角形ABCの面積を利用して円の半径を求めなさい。
(2) 斜線部分の面積の合計を求めなさい。
(3) 三角形ABCの斜線部分以外をAとCを通る直線を軸にして回転させた。えられる立体は点Dが回転する平面に置かれているとします。以下、この平面を地面とします。立体に点Aから光を当てたとき、地面(立体のある部分以外)にできる影の面積を求めなさい。
(4) (3)の立体に点Aの2m下の点Eから光を当てたとき、地面(立体のある部分以外)にできる影の面積は(3)の面積の何倍になるのかを求めなさい。
 (1)
(1)
三角形ABDの面積
=6×8÷2=24
=(6×半径+8×半径+10×半径)÷2
=24×半径÷2
これより、半径=2cm(答え) 2cm
 (2)
(2)
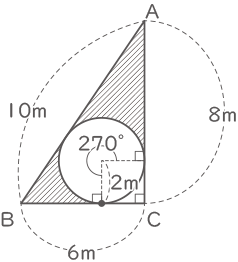
斜線部分の面積の合計
=24-2×2-2×2×3.14×$ \displaystyle \frac{3}{4} $
=10.58cm2(答え) 10.58cm2
 (3)
(3)
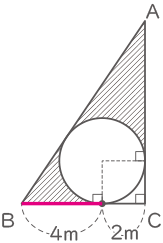
影となるのは赤線の4cmの範囲。
(6×6-2×2)×3.14=100.48cm2(答え) 100.48cm2
 (4)
(4)
CE=BC=6cmなので、三角形ABCと赤線の三角形は合同、ゆえにDF=6cm。
点Eからの光で出来る影の面積は、
(8×8-2×2)×3.14=60×3.14
よって、
$ \displaystyle \frac{60×3.14}{32×3.14} $=$ \displaystyle \frac{15}{8} $=1$ \displaystyle \frac{7}{8} $倍(答え) 1$ \displaystyle \frac{7}{8} $倍

 (1)
(1) (2)
(2) (3)
(3) (4)
(4)