問題
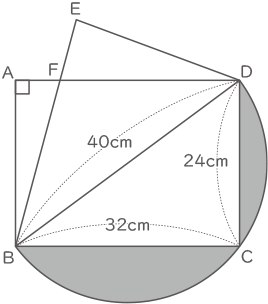次の図は，たて24cm，横32cm，対角線の長さが40cmの長方形ABCDである。また，BDを直径とする半円を図のようにかくと点Cは半円上にある。このとき，次の問いに答えなさい。
ただし，円周率は3.14とする。
（1） かげのついた部分の周りの長さを求めなさい。
（2） かげのついた部分の面積を求めなさい。
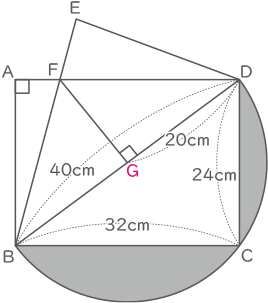
（3） 長方形ABCDをBDを折り目として折り返したとき，頂点Cの移る点をE，BEとADの交点をFとする。このとき，三角形BDFの面積を求めなさい。
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適！ 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
次の図は，たて24cm，横32cm，対角線の長さが40cmの長方形ABCDである。また，BDを直径とする半円を図のようにかくと点Cは半円上にある。このとき，次の問いに答えなさい。
ただし，円周率は3.14とする。（1） かげのついた部分の周りの長さを求めなさい。
（2） かげのついた部分の面積を求めなさい。
（3） 長方形ABCDをBDを折り目として折り返したとき，頂点Cの移る点をE，BEとADの交点をFとする。このとき，三角形BDFの面積を求めなさい。（1）
40×3.14×$ \displaystyle \frac{1}{2} $＋24＋32＝118.8cm（答え） 118.8cm
（2）
（20×20×3.14－24×32）÷2＝244cm2（答え） 244cm2
（3）
三角形ABDと三角形EDBは合同なので、FからBDへ垂直となる線を下してできる交点GはBDの真ん中になる。
三角形ABDと三角形GFDは相似となり、
FG：GD＝BA：ADからFG＝15cm
三角形BDFの面積=15×20÷2×2＝300cm2（答え） 300cm2
（3）
