問題
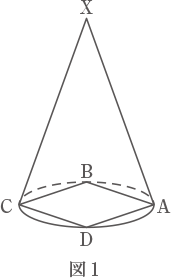 図1のような円すいがあります。この円すいの側面を直線XAに沿って切りひらくと,円の4分の1であるおうぎの形になります。また,円すいの底面の円には,すべての頂点が円周上にあるような正方形ABCDが書いてあります。正方形ABCDの1辺の長さは10cmです。
図1のような円すいがあります。この円すいの側面を直線XAに沿って切りひらくと,円の4分の1であるおうぎの形になります。また,円すいの底面の円には,すべての頂点が円周上にあるような正方形ABCDが書いてあります。正方形ABCDの1辺の長さは10cmです。
(1) XAの長さは底面の円の半径の長さの何倍ですか。
この円すいの表面上を動く点Pと点Qを考えます。
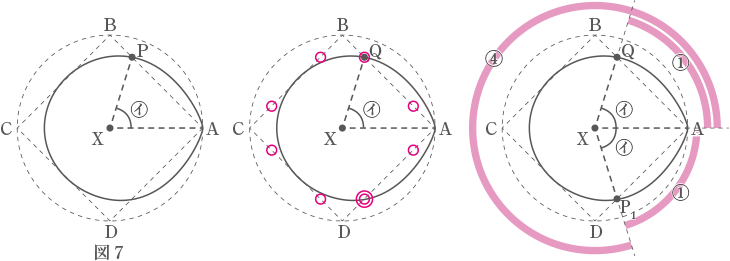
点Pは,図2のように,Aを出発して円すいの側面を最短距離(きょり)で左回りに1周してAに戻(もど)ってきます。一方,点Qは,図3のように,Aを出発して正方形ABCDの辺上を左回りに1周してAに戻ってきます。点Pと点Qは同時にAを出発して,それぞれ一定の速さで動きます。点Pの速さは点Qの速さの4倍です。このとき,円すいを真上から見ると,点Pは図4の実線部分に沿って動いていました。
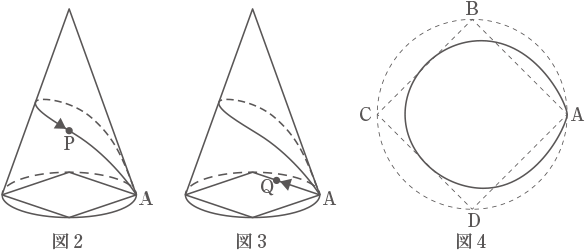
(2) 点PがAを出発してから,再びAに戻るまでに移動した距離を答えなさい。また,点PがAに戻ったときの点Qの位置を,次の①~⑧の中から選び,記号で答えなさい。
① A ② AとBの間 ③ B ④ BとCの間
⑤ C ⑥ CとDの間 ⑦ D ⑧ DとAの間
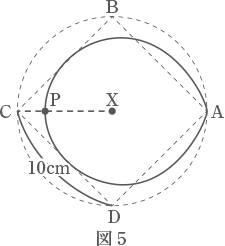 (3) 図5は,あるときに円すいを真上から見た図で,3点C,P,Xは一直線上にありました。
(3) 図5は,あるときに円すいを真上から見た図で,3点C,P,Xは一直線上にありました。
このとき,実際のXPの長さ(円すいの頂点から点Pまでの長さ)と,図 5のXPの長さ (真上から見たときの XPの長さ)を答えなさい。
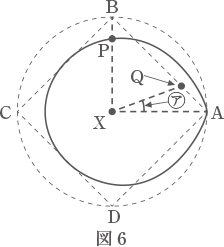 (4) 図6は,あるときに円すいを真上から見た図で,3点B,P,Xは一直線上にありました。
(4) 図6は,あるときに円すいを真上から見た図で,3点B,P,Xは一直線上にありました。
(ア)Aを出発してからこのときまでにかかった時間は,点Pが1周する時間の 倍の時間と比べて,長いですか,短いですか,同じですか。次の①~③の中から選び,記号で答えなさい。
① 長い ② 短い ③ 同じ
(イ) 図6の㋐の角度を答えなさい。
(ウ) 図6のXPの長さは,図6のXQの長さと比べて,長いですか,短いですか, 同じですか。次の①~③の中から選び,記号で答えなさい。また,その理由も書きなさい。
① 長い ② 短い ③ 同じ
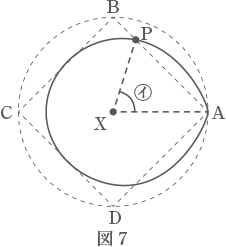 (5) 図7は,あるときに円すいを真上から見た図で,点Pは辺AB 上にありました。図7 の㋑の角度を答えなさい。
(5) 図7は,あるときに円すいを真上から見た図で,点Pは辺AB 上にありました。図7 の㋑の角度を答えなさい。
試験で使われる問題用紙はかなり大きめ。同じ大きさで過去問を用意して本番感覚を養いましょう。印刷するのはパパとママの役目。A3ノビまで対応、全色顔料インクで滲まない。最大給紙枚数は550枚。
解答
- 解答を開く
-
 図1のような円すいがあります。この円すいの側面を直線XAに沿って切りひらくと,円の4分の1であるおうぎの形になります。また,円すいの底面の円には,すべての頂点が円周上にあるような正方形ABCDが書いてあります。正方形ABCDの1辺の長さは10cmです。
図1のような円すいがあります。この円すいの側面を直線XAに沿って切りひらくと,円の4分の1であるおうぎの形になります。また,円すいの底面の円には,すべての頂点が円周上にあるような正方形ABCDが書いてあります。正方形ABCDの1辺の長さは10cmです。(1) XAの長さは底面の円の半径の長さの何倍ですか。
この円すいの表面上を動く点Pと点Qを考えます。
点Pは,図2のように,Aを出発して円すいの側面を最短距離(きょり)で左回りに1周してAに戻(もど)ってきます。一方,点Qは,図3のように,Aを出発して正方形ABCDの辺上を左回りに1周してAに戻ってきます。点Pと点Qは同時にAを出発して,それぞれ一定の速さで動きます。点Pの速さは点Qの速さの4倍です。このとき,円すいを真上から見ると,点Pは図4の実線部分に沿って動いていました。
(2) 点PがAを出発してから,再びAに戻るまでに移動した距離を答えなさい。また,点PがAに戻ったときの点Qの位置を,次の①~⑧の中から選び,記号で答えなさい。
① A ② AとBの間 ③ B ④ BとCの間
⑤ C ⑥ CとDの間 ⑦ D ⑧ DとAの間 (3) 図5は,あるときに円すいを真上から見た図で,3点C,P,Xは一直線上にありました。
(3) 図5は,あるときに円すいを真上から見た図で,3点C,P,Xは一直線上にありました。
このとき,実際のXPの長さ(円すいの頂点から点Pまでの長さ)と,図 5のXPの長さ (真上から見たときの XPの長さ)を答えなさい。 (4) 図6は,あるときに円すいを真上から見た図で,3点B,P,Xは一直線上にありました。
(4) 図6は,あるときに円すいを真上から見た図で,3点B,P,Xは一直線上にありました。(ア)Aを出発してからこのときまでにかかった時間は,点Pが1周する時間の 倍の時間と比べて,長いですか,短いですか,同じですか。次の①~③の中から選び,記号で答えなさい。
① 長い ② 短い ③ 同じ
(イ) 図6の㋐の角度を答えなさい。
(ウ) 図6のXPの長さは,図6のXQの長さと比べて,長いですか,短いですか, 同じですか。次の①~③の中から選び,記号で答えなさい。また,その理由も書きなさい。
① 長い ② 短い ③ 同じ
 (5) 図7は,あるときに円すいを真上から見た図で,点Pは辺AB 上にありました。図7 の㋑の角度を答えなさい。
(5) 図7は,あるときに円すいを真上から見た図で,点Pは辺AB 上にありました。図7 の㋑の角度を答えなさい。(1)
円すいの性質より、$ \displaystyle \frac{90°}{360°} $=$ \displaystyle \frac{底面の円の半径}{母線} $となる。よって、XAの長さは底面の円の半径の長さの4倍。(答え) 4倍
補足(2)
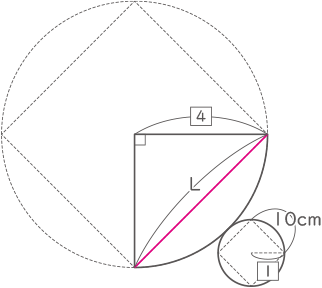
正方形の面積が平方数となれば一辺の長さが分かることを利用する。 図の円すいの展開図で、小さい円の半径を1⃣、点Pが移動した距離(最短距離)をLとする。
図の円すいの展開図で、小さい円の半径を1⃣、点Pが移動した距離(最短距離)をLとする。
小さい正方形の面積は100cm2で、1⃣×1⃣×2でも求められるので1⃣×1⃣=50cm2となる。
また、L×Lで求められる大きい正方形の面積は、4⃣×4⃣×2と同じ。
1⃣×1⃣=50cm2とわかっているので、
L×L=(1⃣×4)×(1⃣×4)×2=50×4×4×2=40×40であり、L=40cmとなる。
Pが1周(40cm)移動するのであれば、1/4の速さのQは10cm移動し、B(③)にくる。(答え) Pの移動距離は40cm , Qの位置は③
補足(3)
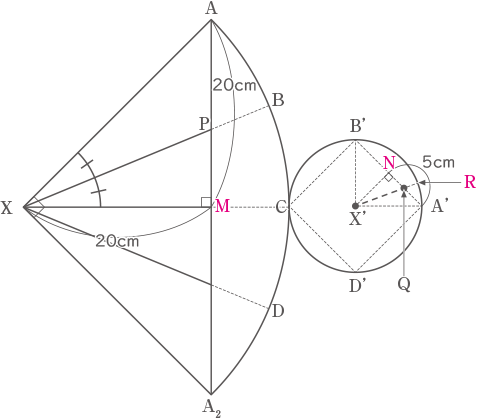
実際のXPの長さ(円すいの頂点から点Pまでの長さ)は、円すいの展開図より20cmとわかる。
図 5のXPの長さ (真上から見たときの XPの長さ)は、円すいを側面から見たときの比で5cmとわかる。
(答え) 実際のXPの長さは20cm , 図 5のXPの長さは5cm
(4)-(ア)
 図より、Aを出発してからXB上にくるまでの距離の方が長い。よって時間もかかる。・・・①
図より、Aを出発してからXB上にくるまでの距離の方が長い。よって時間もかかる。・・・①(答え) ①
(4)-(イ)
補助線とM,N,Rを追記する。
三角形AMXと三角形A’NX’は相似であり、点PがAから20cm進みMにくると、点Qは の速さなのでA’から5cm進みNにくる。よって、AP:PM=A’Q:QNとなり、角AXP=角A’X’Q=22.5°とわかる。
(答え) 22.5°
(4)-(ウ)
(答え) ③
理由:前問(4)-(イ)の図より、三角形AXPと三角形A’X’Qは相似となり、おうぎ型AXBとおうぎ型A’X’Rも相似になる。よって、XP:PB=X’Q:QRとなり、上から見たXPの長さはX’Qの長さと同じになる。(5)
(4)-(イ)の図より、- おうぎ型X’A’B’とおうぎ型XAA2は相似
- AA2が40cmでA’B’が10cm、速さの比がP:Q=4:1より、AP:PA2=A’Q:QB’となる(→上から見ると、角A’X’Q:角AXP=1:4なのでPの角度はQの角度の4倍進む)
- XP:X’Q=4:1となる(→上から見ると、XP=X’Q)
(再びQを利用する)
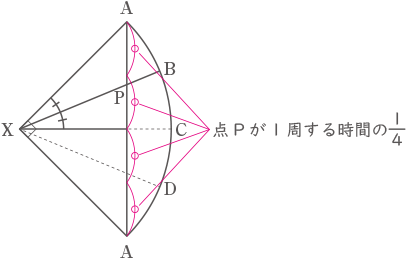
上記を踏まえ、図7のPの位置にQが来た場合を考えると、XQとXPの長さは同じになるので赤丸8カ所のうち赤い二重丸がPの来たところ。角度の比が①:④なので、㋑=①=360÷⑤=72°

(答え) 72°


 図の円すいの展開図で、小さい円の半径を1⃣、点Pが移動した距離(最短距離)をLとする。
図の円すいの展開図で、小さい円の半径を1⃣、点Pが移動した距離(最短距離)をLとする。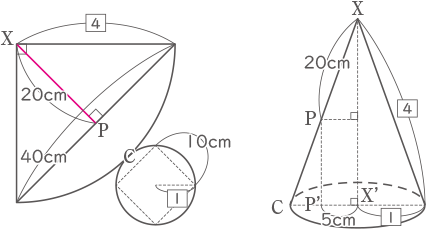
 図より、Aを出発してからXB上にくるまでの距離の方が長い。よって時間もかかる。・・・①
図より、Aを出発してからXB上にくるまでの距離の方が長い。よって時間もかかる。・・・①