問題
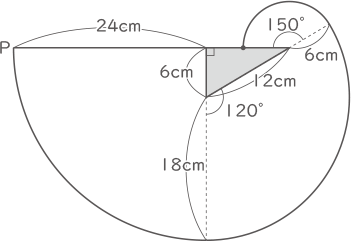
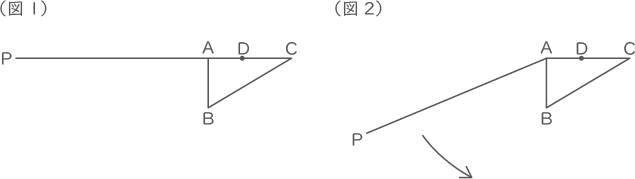
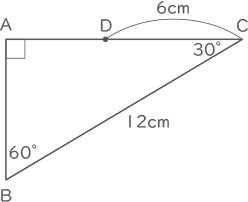
図1は角Aが90゜、角Bが60°、BCの長さが12cmの直角三角形ABCの点Aから先端(せんたん)をPとする糸を角PABが90゜になるようにぴんと張った図です。図2のように反時計回りに糸をぴんと張ったまま直角三角形ABCに巻きつけていったところ、AB、BCの順に巻きついた後、AC上の点Cから6cmの点DにPが重なりました。
このとき、次の問いに答えなさい。ただし、円周率を3.14とします。
(1) 糸の長さ(APの長さ)を求めなさい。
(2) 糸の先端Pが通った経路の長さを求めなさい。
(3) 糸が通った部分の面積を求めなさい。
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適! 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
図1は角Aが90゜、角Bが60°、BCの長さが12cmの直角三角形ABCの点Aから先端(せんたん)をPとする糸を角PABが90゜になるようにぴんと張った図です。図2のように反時計回りに糸をぴんと張ったまま直角三角形ABCに巻きつけていったところ、AB、BCの順に巻きついた後、AC上の点Cから6cmの点DにPが重なりました。

このとき、次の問いに答えなさい。ただし、円周率を3.14とします。
(1) 糸の長さ(APの長さ)を求めなさい。
(2) 糸の先端Pが通った経路の長さを求めなさい。
(3) 糸が通った部分の面積を求めなさい。 (1)
(1)
三角定規と辺の長さの比が同じであり、AB:BC=1:2を使うとABは6cm。
よってAPの長さは6+12+6=24cm(答え) 24cm
(2)
糸の先端Pが通った経路は下図の様になる。求める長さ=24×2×3.14×$ \displaystyle \frac{90}{360} $+18×2×3.14×$ \displaystyle \frac{120}{360} $+6×2×3.14×$ \displaystyle \frac{150}{360} $
=91.06cm
(答え) 91.06cm
(3)
(2)の図より、
求める面積=24×24×3.14×$ \displaystyle \frac{90}{360} $+18×18×3.14×$ \displaystyle \frac{120}{360} $+6×6×3.14×$ \displaystyle \frac{150}{360} $
=838.38cm2(答え) 838.38cm2

 (1)
(1)