数の並び方-3-1（慶應義塾中等部2022/つくることができない最大の整数は？）

1 問題
2 解答

問題

問題（慶應義塾中等部2022/つくることができない最大の整数は？）

次の□に適当な数を入れなさい。

（1） 5＋6＝11，5＋6 + 6＝17のように、5と6をいくつかずつ加えて整数をつくります。また、5＋5＝10，6＋6＝12 のように、5または6のどちらか一方の数のみを加えてもよいこととします。このとき、つくることができない最大の整数は□です。

（2） 11＋13＝24のように、11と13をいくつかずつ加えて整数をつくります。11も13も必ず1つは加えるとき、つくることができない最大の整数は□です。

灘をはじめ、名だたる難関中学に毎年多数の合格者を出す「浜学園」。講師の質や、教材のよさは折り紙付き。引きつりそうな料金設定ですが、中学受験をすると決めたら偏差値を買うんだ！ぐらいの前向きな気持ちで行きましょう。気になる方は資料請求してお子さんに合いそうか是非確認してみましょう。もちろん、体験入塾も無料で用意されています。

解答

解答を開く

次の□に適当な数を入れなさい。

（2） 11＋13＝24のように、11と13をいくつかずつ加えて整数をつくります。11も13も必ず1つは加えるとき、つくることができない最大の整数は□です。

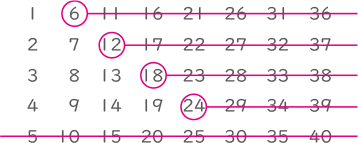
（1）
①、5ずつ折り返す列を作る。
②、最下行の５の倍数を消す。
③、丸を付けた６の倍数を消す。
④、③で丸を付けた数字の右側は5を何度か足した数になるので消す。

条件に合う最大の整数は19となる。

別解
特定の条件下であれば下記の式も使える。
5×6－5－6＝19

（答え）　19

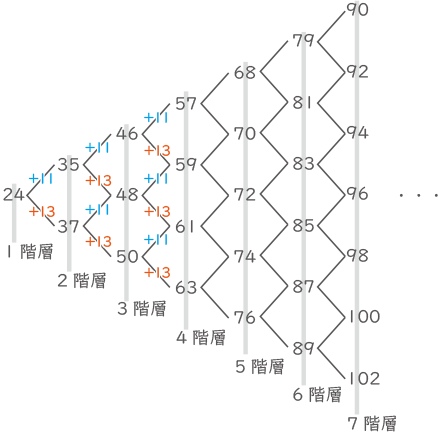
（2）
11も13必ず使うので、24から階層をつくる。

規則に従って以降の数字も並べていく。
1階層　24
2階層　35～37
3階層　46～50
4階層　57～63
5階層　68～76
6階層　79～89
7階層　90～102
8階層　101～115
9階層　112～128
10階層　123～141
11階層　134～154
12階層　145～167
13階層　156～180
14階層　167～193
15階層　178～206
16階層　189～219
…