問題
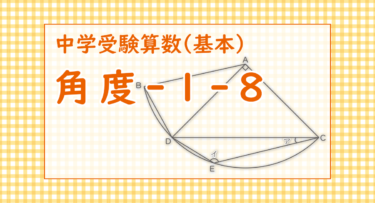
図のように,おうぎ形ABCの中に3つの三角形があります。
辺BDと辺DE,辺ACと辺CEはそれぞれ等しい長さです。
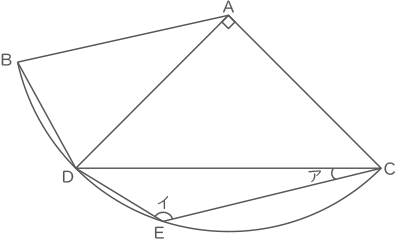
(1) 角アの大きさと角イの大きさはそれぞれ何度ですか。
(2) 三角形ADCの面積が12cm2のとき,三角形ABDの面積は何cm2ですか。
灘をはじめ、名だたる難関中学に毎年多数の合格者を出す「浜学園」。講師の質や、教材のよさは折り紙付き。引きつりそうな料金設定ですが、中学受験をすると決めたら偏差値を買うんだ!ぐらいの前向きな気持ちで行きましょう。気になる方は資料請求してお子さんに合いそうか是非確認してみましょう。もちろん、体験入塾も無料で用意されています。
解答
- 解答を開く
-
図のように,おうぎ形ABCの中に3つの三角形があります。
辺BDと辺DE,辺ACと辺CEはそれぞれ等しい長さです。
(1) 角アの大きさと角イの大きさはそれぞれ何度ですか。
(2) 三角形ADCの面積が12cm2のとき,三角形ABDの面積は何cm2ですか。(1)
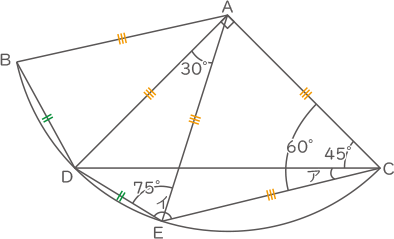
同じ長さの線に印をつける。
ACEは正三角形なので、ア=60-45=15度
ADEは二等辺三角形なので、それぞれ30度と75度となり、イ=75+60=135度
(答え) ア 15度 イ 135度
(2)
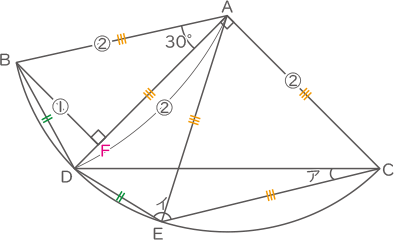
(1)より角BADは30度とわかる。
補助線を引くとABFは正三角形の半分の図形と分かるので、BFはおうぎ形の半径(②とする)の半分(①とする)の長さとなる。
また、三角形ADCの面積は12cm2で②×②×$ \displaystyle \frac{1}{2} $と表せる。
よって、三角形ABDの面積=②×①×$ \displaystyle \frac{1}{2} $=②×②×$ \displaystyle \frac{1}{2} $×$ \displaystyle \frac{1}{2} $=12×$ \displaystyle \frac{1}{2} $=6cm2
(答え) 6cm2