問題
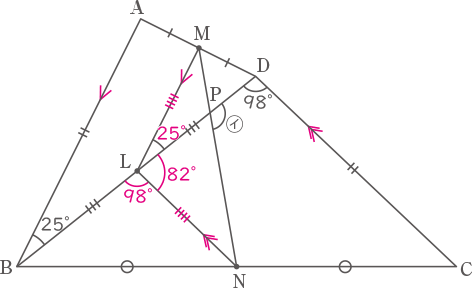
下の図のような,AB=CD,AM=MD,BN=NCの四角形ABCDにおいて,2直線BDとMNの交点をP,BDの真ん中の点をLとする。このとき,次の間いに答えなさい。
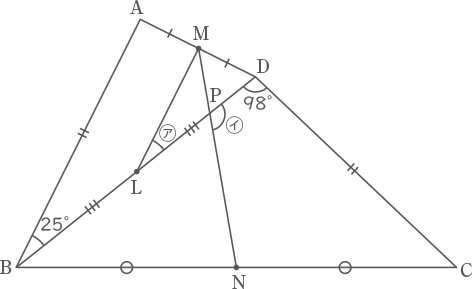
(1) 角㋐の大きさを求めなさい。
(2) 角㋑の大きさを求めなさい。
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適! 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
下の図のような,AB=CD,AM=MD,BN=NCの四角形ABCDにおいて,2直線BDとMNの交点をP,BDの真ん中の点をLとする。このとき,次の間いに答えなさい。

(1) 角㋐の大きさを求めなさい。
(2) 角㋑の大きさを求めなさい。与えられた条件は
① AB=CD
② AM=MD
③ BN=NC
④ BL=LD
の4つと2つの角度。(1)
三角形ABDにおいて、点Mは辺ADの中点、点LはBDの中点。よって、ABとMLは平行とわかり、角ABDと角MLDは同位角の関係にある。角MLD(㋐)は25°。(答え) 25°
(2)
②と④の条件は(1)で使ったので、①と③の条件の使い方を考える。
三角形BCDにおいて、点LはBDの中点、点NはBCの中点。よって、CDとNLは平行で、
LMとLNは長さが等しく、三角形LNMは二等辺三角形とわかる。
角BDCと角BLNは同位角の関係にあるので98°
角DLNは180-98=82°
二等辺三角形LNMの角LNMは{180-(25+82)}÷2=36.5°
㋑=82+36.5=118.5°(答え) 118.5°