問題
問題(台形内のさっ角と二等辺三角形)
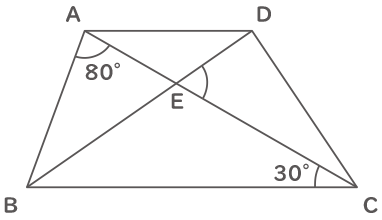
図の様な台形ABCDに線分ACと線分BDがあり、その交点をEとします。AB=ADのとき、角CEDは何度ですか。
【家庭学習】過去問をA3で実サイズコピーして本番形式で臨みましょう
4.45
試験で使われる問題用紙はかなり大きめ。同じ大きさで過去問を用意して本番感覚を養いましょう。印刷するのはパパとママの役目。A3ノビまで対応、全色顔料インクで滲まない。最大給紙枚数は550枚。
解答
- 解答を開く
-
図の様な台形ABCDに線分ACと線分BDがあり、その交点をEとします。AB=ADのとき、角CEDは何度ですか。

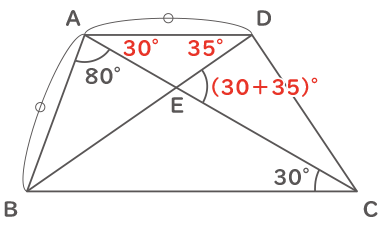
線分ADと線分BCが平行なので錯角(さっかく)となる角ACBと角CADは両方とも30°となる。また、AB=ADより三角形ABDは二等辺三角形なので角ADB={180-(80+30)}÷2=35°となる。よって三角形AEDの外角となる角CEDは30+35=65より65度。

(答え)65度
ではまた~