問題
図のような四角柱ABCD-EFGHがあり、底面は1辺が4cmのひし形です。また、点Pと点Qはそれぞれ辺AB,BCの真ん中の点で、点Rは辺BF上にありBRの長さが1cmです。この四角柱を平面上に置き、点Dから6cm真上のところにある電球Oでこの四角柱に光を当てます。
このとき、次の各問いに答えなさい。
なお、必要があれば、正三角形の高さは、1辺の長さの0.87倍として計算しなさい。
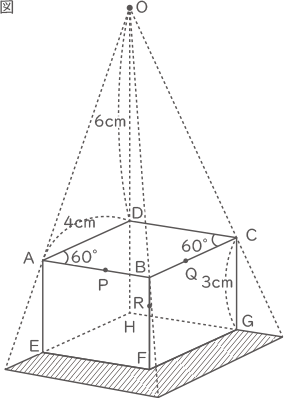
(1) 平面上にできるかげ(図のしゃ線部分)の面積は何cm2ですか。
(2) 3点P,Q,Rを通る平面でこの四角柱を切り、点Bを含む立体を取りのぞくと、平面上にできるかげの面積は何cm2になりますか。
(3) さらに3点P,Q,Fを通る平面でこの立体を切り、点Rを含む立体を取りのぞくと、平面上にできるかげの面積は何cm2になりますか。
これまでほとんどの通信教育で実現できなかった難関国私立中学合格。Z会なら、可能です。【公立中高一貫校を受検予定 】の方は試しに資料請求してみましょう。HPにも「小学生コース専科 公立中高一貫校受検対策講座のご案内」が詳しく記載されています。
解答
- 解答を開く
-
図のような四角柱ABCD-EFGHがあり、底面は1辺が4cmのひし形です。また、点Pと点Qはそれぞれ辺AB,BCの真ん中の点で、点Rは辺BF上にありBRの長さが1cmです。この四角柱を平面上に置き、点Dから6cm真上のところにある電球Oでこの四角柱に光を当てます。
このとき、次の各問いに答えなさい。
なお、必要があれば、正三角形の高さは、1辺の長さの0.87倍として計算しなさい。
(1) 平面上にできるかげ(図のしゃ線部分)の面積は何cm2ですか。
(2) 3点P,Q,Rを通る平面でこの四角柱を切り、点Bを含む立体を取りのぞくと、平面上にできるかげの面積は何cm2になりますか。
(3) さらに3点P,Q,Fを通る平面でこの立体を切り、点Rを含む立体を取りのぞくと、平面上にできるかげの面積は何cm2になりますか。
(1)
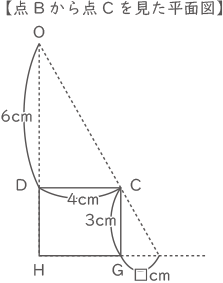
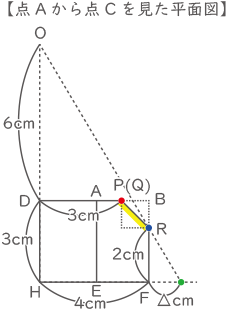
【点Bから点Cを見た平面図】
点Aから点Cを見た平面図も同じ形になり、点Bから点Aを見た平面図はOHを対象の軸として線対象な図形となる。
6:4=3:□、
□=12÷6=2cm

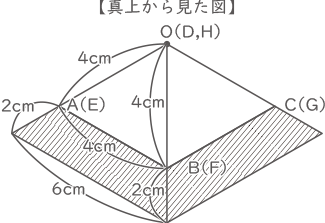
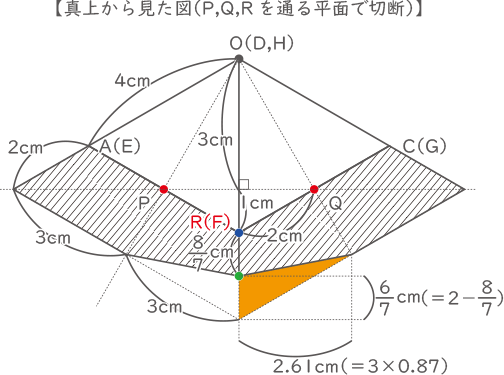
【真上から見た図】より、ひし形と影をあわせた図形もひし形とわかる。
かげの面積=ひし形の面積×$ \displaystyle \frac{6}{4} $×$ \displaystyle \frac{6}{4} $-ひし形の面積=ひし形の面積×($ \displaystyle \frac{9}{4} $-1)
ひし形の面積=4×4×0.87×$ \displaystyle \frac{1}{2} $×2=16×0.87
かげの面積=16×0.87×$ \displaystyle \frac{5}{4} $=17.4cm2(答え) 17.4cm2
(2)

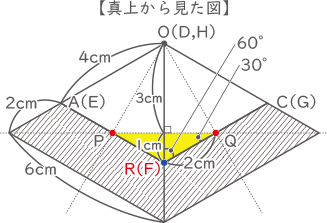
黄色の部分が切断面で、真上から見ると正三角形の半分が2つ接した形になっている。
 PRの傾斜よりORの傾斜の方が大きいので、点Rによってかげの先端がつくられる。
PRの傾斜よりORの傾斜の方が大きいので、点Rによってかげの先端がつくられる。
7:4=2:△、
△=8÷7=$ \displaystyle \frac{8}{7} $cm オレンジの部分は図形の切断によりかげが減ったところで、1辺3cmの正三角形の一部になっている。
オレンジの部分は図形の切断によりかげが減ったところで、1辺3cmの正三角形の一部になっている。
よって、減ったかげの面積は(3×0.87)×(2-$ \displaystyle \frac{8}{7} $)×$ \displaystyle \frac{1}{2} $×2=2$ \displaystyle \frac{83}{350} $
求めるかげの面積=17.4-2$ \displaystyle \frac{83}{350} $=15$ \displaystyle \frac{57}{350} $(答え) 15$ \displaystyle \frac{57}{350} $cm2(3)

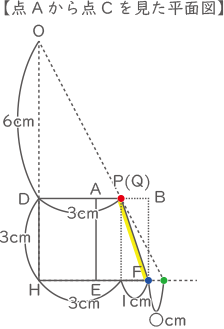
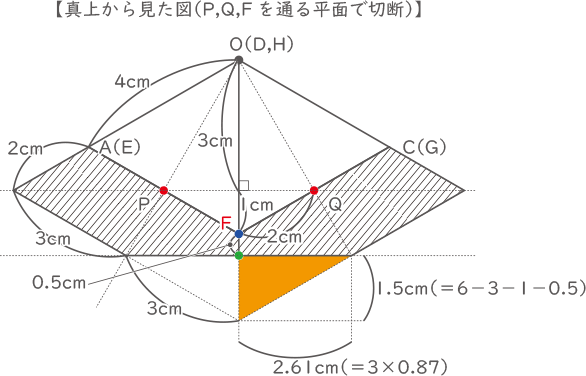
OPの傾斜よりPFの傾斜の方が大きいので、点Pによってかげの先端がつくられる。
6:3=3:(1+○)
1+○=9÷6=1.5
○=0.5cm
オレンジの部分は図形の切断によりかげが減ったところで、1辺3cmの正三角形の半分になっている。
よって、減ったかげの面積は(3×0.87)×1.5×$ \displaystyle \frac{1}{2} $×2=2.61×1.5=3.915
求めるかげの面積=17.4-3.915=13.485(答え) 13.485cm2