過不足算-1-2（赤玉と白玉の数を求める）

問題

解答

 解答を開く

 

何人かの生徒に赤玉と、赤玉より20個少ない白玉を配ります。
赤玉を7個ずつ配ると22個足りず、白玉を4個ずつ配ると69個余ります。
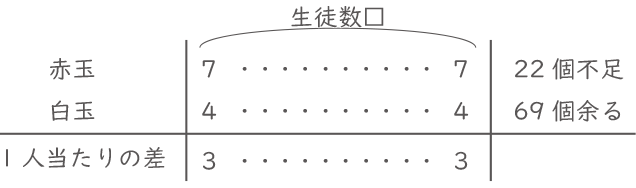
赤玉、白玉の個数と、生徒数を求めなさい。

 

---

 

図表をつくってみる。

 

 

赤玉の数は生徒数×7個－22個で、白玉の数は生徒数×4個＋69個となり、その差が20個となるので赤玉と白玉の差は、
（7個－4個）×生徒数－22個－69個＝20個、
3×□－91＝20，　3×□＝111，　□＝37。よって生徒数は37人。
赤玉＝7個×37人－22個＝237個，
白玉＝4個×37人＋69個＝217個。

 

（答え）赤玉237個，白玉217個，生徒数37人

 

 別解を開く

 

何人かの生徒に赤玉と、赤玉より20個少ない白玉を配ります。
赤玉を7個ずつ配ると22個足りず、白玉を4個ずつ配ると69個余ります。
赤玉、白玉の個数と、生徒数を求めなさい。

 

---

 

理解しやすい数に変えてしまう。
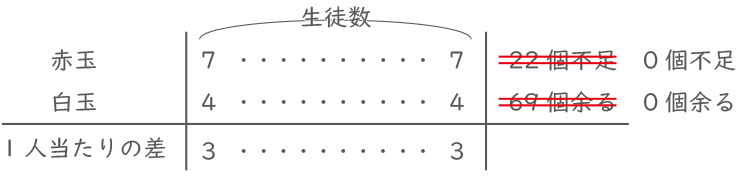
そもそも赤玉と白玉の過不足が数え難くしているので、過不足を無くしてしまう。

 

 

赤玉を22個増やせば22個の不足は無くなり、赤玉－白玉＝20＋22＝42個となる。さらに、白玉を69個減らせば69個の余りも無くなり、赤玉－白玉＝42＋69＝111個となる。これで、赤玉も白玉もぴったりの数を生徒に配ることができて、過不足も出ない。
この111個が1人当たりの差×生徒数なので、生徒数＝111÷3＝37人とわかる。
数を戻して、赤玉＝7×37－22＝237個，白玉＝4×37＋69＝217個となる。

 

（答え）赤玉237個，白玉217個，生徒数37人