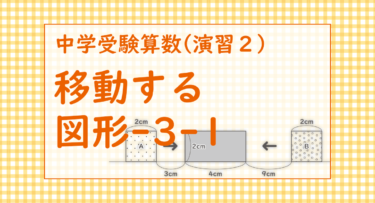
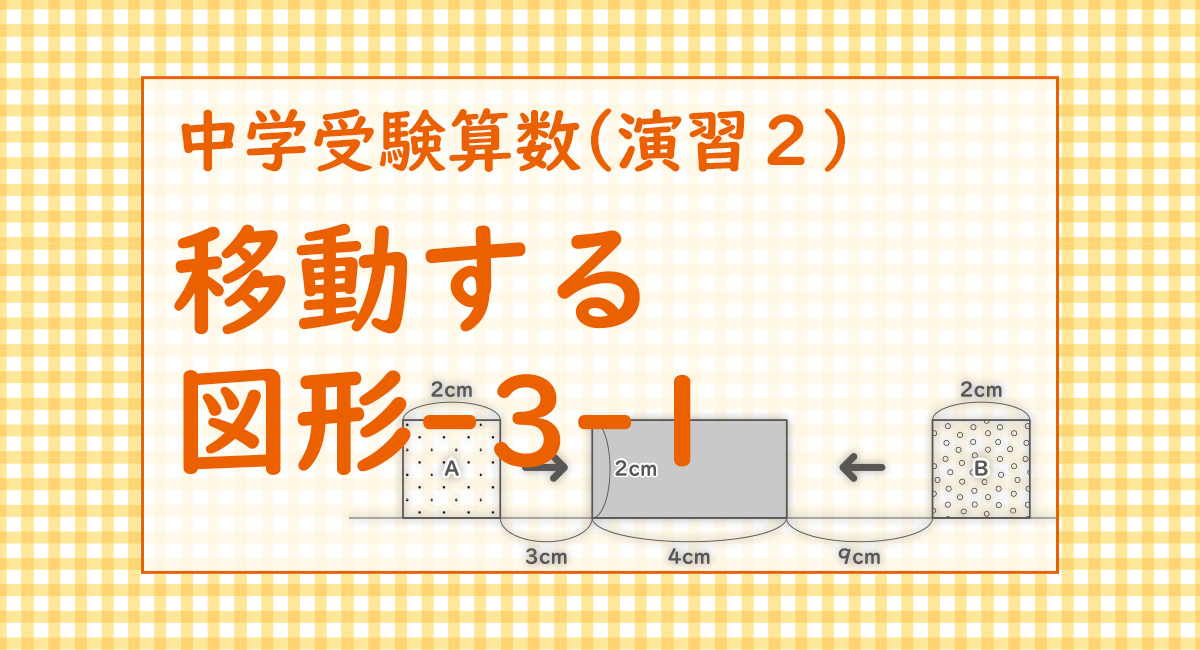
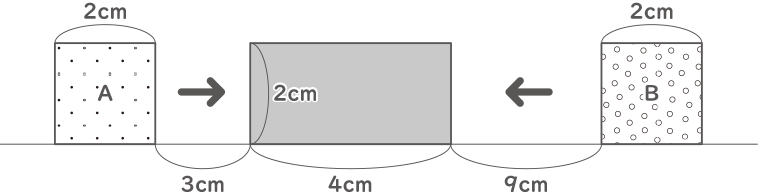
移動する図形-3-1（3つの図形の重なる部分の面積が一番大きくなる時）

1 問題
2 解答

問題

問題（3つの図形の重なる部分の面積が一番大きくなる時）

図の様な2つの正方形A・Bと長方形があり、直線に沿って正方形Aは右側へ毎秒1cmの速さで、正方形Bは左側へ毎秒3cmの速さで動きます。
（1）　正方形Aと正方形Bが出会うのは何秒後ですか。
（2）　3つの図形が重なった部分の面積が一番大きいのは何cm²のときですか。

これまでほとんどの通信教育で実現できなかった難関国私立中学合格。Z会なら、可能です。【公立中高一貫校を受検予定】の方は試しに資料請求してみましょう。HPにも「小学生コース専科　公立中高一貫校受検対策講座のご案内」が詳しく記載されています。

解答

解答を開く

（1）
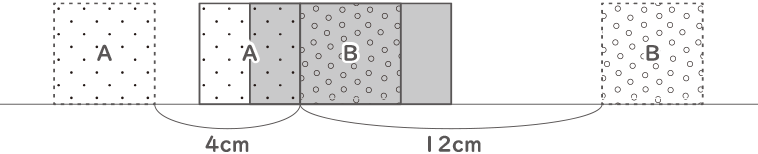
正方形Aと正方形Bは16cm離れているので、出会うのは16÷(1＋3)＝4秒後で、図の様になる。

（答え）　4秒後

（2）

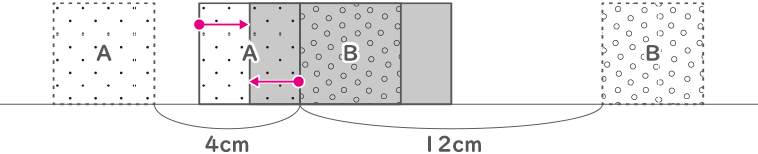
（1）の2つの正方形が出会った図で動きを見てみると、
【正方形A】の最後尾が長方形の左はしに来るのはこの図から1秒後。
【正方形B】の先頭が長方形の左はしに来るのはこの図から$ \displaystyle \frac{1}{3} $秒後。
よって、【正方形B】の方が早く長方形の左はしに来るので、その時を次の図で考える。

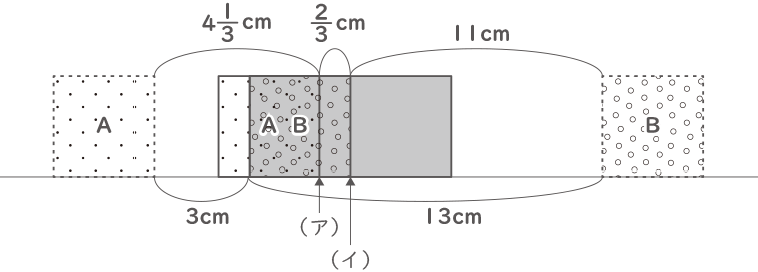
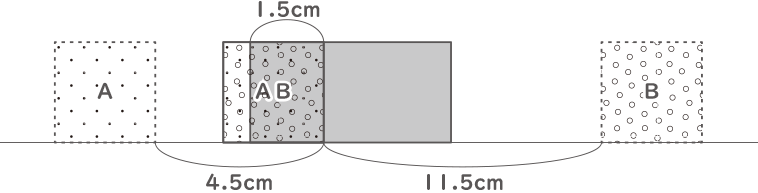
正方形Bの先頭が長方形の左はじにくるのが、図の様に動き始めてから$ \displaystyle \frac{13}{3} $秒後になる。
その時、正方形Aは1×$ \displaystyle \frac{13}{3} $＝4$ \displaystyle \frac{1}{3} $cm動いているので、（ア）から（イ）までは（3＋4＋9）－11－4$ \displaystyle \frac{1}{3} $＝$ \displaystyle \frac{2}{3} $cmとわかる。
よって、正方形Aの先頭（ア）と正方形Bの最後尾（イ）が出会うときが、3つの図形が重なった部分の面積が一番大きくなる。
動き始めてから、$ \displaystyle \frac{13}{3} $＋$ \displaystyle \frac{2}{3} $÷（1＋3）＝4.5秒後に、次の図の様に面積が一番大きくなる。