問題
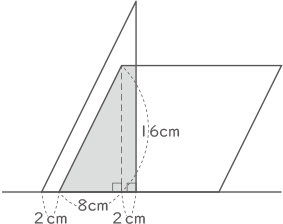
図のように，直線上に直角三角形と平行四辺形があります。図の位置から直角三角形は動かさずに，平行四辺形を毎秒2cmの速さで左へ動かしたとき，2つの図形の重なった部分の面積をSとします。
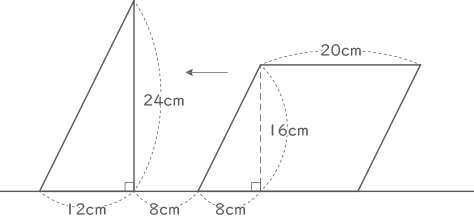
次の問いに答えなさい。
（1） 動き始めてから9秒後の面積Sを求めなさい。
（2） 動き始めてから15秒後の面積Sを求めなさい。
（3） 面積Sが64cm2になるのは，動き始めてから何秒後と何秒後ですか。
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適！ 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
図のように，直線上に直角三角形と平行四辺形があります。図の位置から直角三角形は動かさずに，平行四辺形を毎秒2cmの速さで左へ動かしたとき，2つの図形の重なった部分の面積をSとします。
次の問いに答えなさい。
（1） 動き始めてから9秒後の面積Sを求めなさい。
（2） 動き始めてから15秒後の面積Sを求めなさい。
（3） 面積Sが64cm2になるのは，動き始めてから何秒後と何秒後ですか。12：24＝8：16より、2つの図形の斜辺は平行となる。
（1）
平行四辺形は9秒で18cm移動する。
面積S＝（10＋2）×16÷2＝96cm2。
（答え） 96cm2
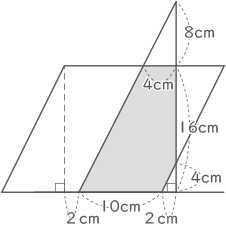
（2）
平行四辺形は15秒で30cm移動する。
面積S＝（4＋12）×16÷２－2×4÷2＝124cm2
（答え） 96cm2
（3）
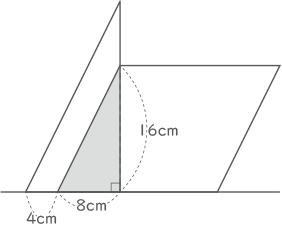
平行四辺形は8秒で16cm移動し、図の様になる。この時の面積は、
S＝8×16÷２＝64cm2
これが1つ目の答えで8秒後。
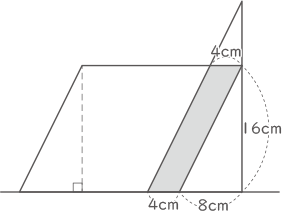
平行四辺形は18秒で36cm移動し、図の様になる。この時の面積は、
S＝4×16＝64cm2
これが2つ目の答えで18秒後。（答え） 8秒後と18秒後
（3）
平行四辺形は18秒で36cm移動し、図の様になる。この時の面積は、
