問題
英子さんは自転車で公園を出発し,途中で休憩(けい)してから駅へ向かいます。
和子さんは自転車で駅から公園まで休まず向かいます。英子さんは常に毎分250mの速さで走り,和子さんも常に一定の速さで走ります。2人は同時に出発してから16分15秒後に出会いました。
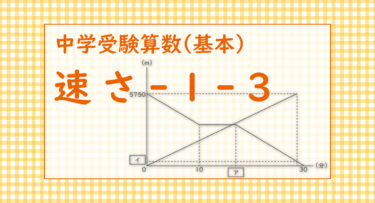
下のグラフは,2人が同時に出発してからの時間(分)と,駅までの距離(きょり)(m)との関係を表したものです。
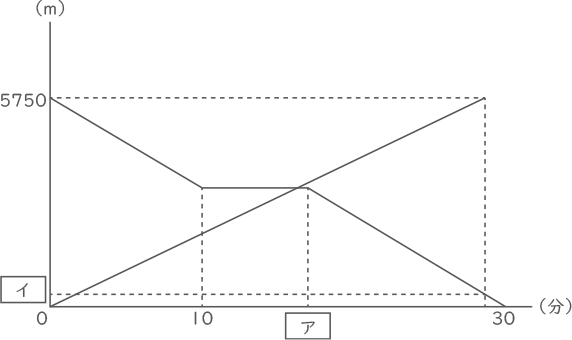
(1) [ ア ]にあてはまる数を答えなさい。
(2) 和子さんの速さは毎分何mですか。
(3) 和子さんが公園に着くのは駅を出発してから何分何秒後ですか。
(4) [ イ ]にてはまる数を答えなさい。
これまでほとんどの通信教育で実現できなかった難関国私立中学合格。Z会なら、可能です。【公立中高一貫校を受検予定 】の方は試しに資料請求してみましょう。HPにも「小学生コース専科 公立中高一貫校受検対策講座のご案内」が詳しく記載されています。
解答
- 解答を開く
-
英子さんは自転車で公園を出発し,途中で休憩(けい)してから駅へ向かいます。
和子さんは自転車で駅から公園まで休まず向かいます。英子さんは常に毎分250mの速さで走り,和子さんも常に一定の速さで走ります。2人は同時に出発してから16分15秒後に出会いました。
下のグラフは,2人が同時に出発してからの時間(分)と,駅までの距離(きょり)(m)との関係を表したものです。
(1) [ ア ]にあてはまる数を答えなさい。
(2) 和子さんの速さは毎分何mですか。
(3) 和子さんが公園に着くのは駅を出発してから何分何秒後ですか。
(4) [ イ ]にてはまる数を答えなさい。(1)
英子さんは休憩しなければ23分(=5750÷250)で駅に着くので、休憩時間は7分(=30-23)。
ア=10+7=17分。(答え) 17
(2)
英子さんが10分で進む距離は2500m(=250×10)なので、和子さんが英子さんに出会ったのは駅から3250m(=5750-2500)のことろ。
よって、和子さんの速さは毎分200m(=3250÷16.25)。(答え) 毎分200m
(3)
5750÷200=28$ \displaystyle \frac{3}{4} $分=28$ \displaystyle \frac{45}{60} $分=28分45秒(答え) 28分45秒
(4)
30分-28分45秒=1.25分
250×1.25=312.5m(答え) 312.5