問題
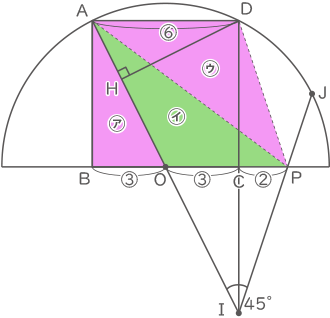
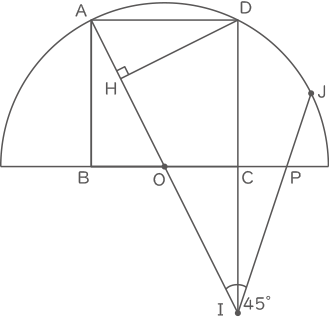 右の図において,点Oは半径5cmの半円の中心です。また,四角形ABCDは正方形です。AIとDHは垂直に交わり,AIとIJは45゜で交わります。
右の図において,点Oは半径5cmの半円の中心です。また,四角形ABCDは正方形です。AIとDHは垂直に交わり,AIとIJは45゜で交わります。
次の問いに答えなさい。
(1) AHとHIの比を求めなさい。
(2) 四角形ABCDの面積を求めなさい。
(3) OCとCPの比を求めなさい。
(4) 三角形DHPの面積を求めなさい。
これまでほとんどの通信教育で実現できなかった難関国私立中学合格。Z会なら、可能です。【公立中高一貫校を受検予定 】の方は試しに資料請求してみましょう。HPにも「小学生コース専科 公立中高一貫校受検対策講座のご案内」が詳しく記載されています。
解答
- 解答を開く
-
 右の図において,点Oは半径5cmの半円の中心です。また,四角形ABCDは正方形です。AIとDHは垂直に交わり,AIとIJは45゜で交わります。
右の図において,点Oは半径5cmの半円の中心です。また,四角形ABCDは正方形です。AIとDHは垂直に交わり,AIとIJは45゜で交わります。
次の問いに答えなさい。(1) AHとHIの比を求めなさい。
(2) 四角形ABCDの面積を求めなさい。
(3) OCとCPの比を求めなさい。
(4) 三角形DHPの面積を求めなさい。 (1)
(1)
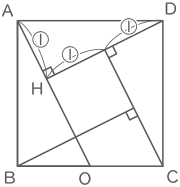
AD:DI=1:2で△AHDと△DHIと△ADIは相似なことより、AHの長さを①とするとHD=②、HI=④、よって、AH:HI=1:4。(答え) 1:4
 (2)
(2)
問(1)より、⑤=10cm,AH(①)=2cm,DH(②)=4cm
四角形ABCDの面積=2×4×2+2×2=20cm2(答え) 20cm2
 (3)
(3)
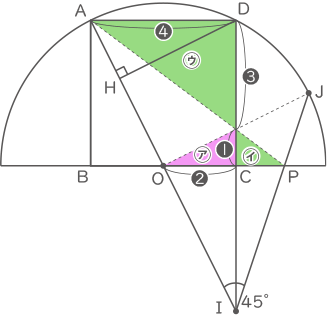
問(1)と同様に考え、㋐の2辺を❶:❷とすると、㋒の2辺は❸:❹となる。
㋐の面積を❶×❷=$ \fbox{2} $、㋒の面積を❸×❹=$ \fbox{12} $とする。
㋑と㋒は相似で辺の比が1:3なので、㋑の面積は$ \fbox{12} $×$ \displaystyle \frac{1}{3} $×$ \displaystyle \frac{1}{3} $=$ \fbox{\( \displaystyle \frac{4}{3} \)} $
㋐の面積:㋑の面積=$ \fbox{2} $:$ \fbox{\( \displaystyle \frac{4}{3} \)} $=3:2
よって、OC:CP=3:2(答え) 3:2
 (4)
(4)
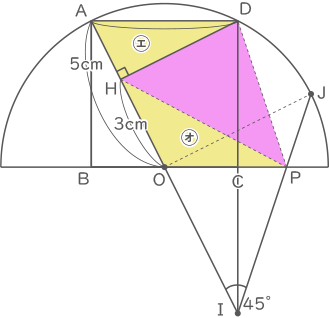
問(3)の比を使い、比をふりなおし、各面の面積を求める。
㋐の面積=20×$ \displaystyle \frac{1}{4} $=5cm2
㋑の面積=5×$ \displaystyle \frac{⑤}{③} $=$ \displaystyle \frac{25}{3} $cm2
㋒の面積=5×$ \displaystyle \frac{⑥}{③} $=10cm2
AOPDの面積=18$ \displaystyle \frac{1}{3} $cm2 ㋓の面積=2×4÷2=4cm2
㋓の面積=2×4÷2=4cm2
㋔の面積=㋑×$ \displaystyle \frac{3}{5} $=5cm2
三角形DHPの面積=18$ \displaystyle \frac{1}{3} $-4-5=9$ \displaystyle \frac{1}{3} $cm2(答え) 9$ \displaystyle \frac{1}{3} $cm2


 (2)
(2) (3)
(3) (4)
(4) ㋓の面積=2×4÷2=4cm2
㋓の面積=2×4÷2=4cm2







