問題
問題(愛光中学2015/(円の半径×円の半径)が面積であることを利用する)
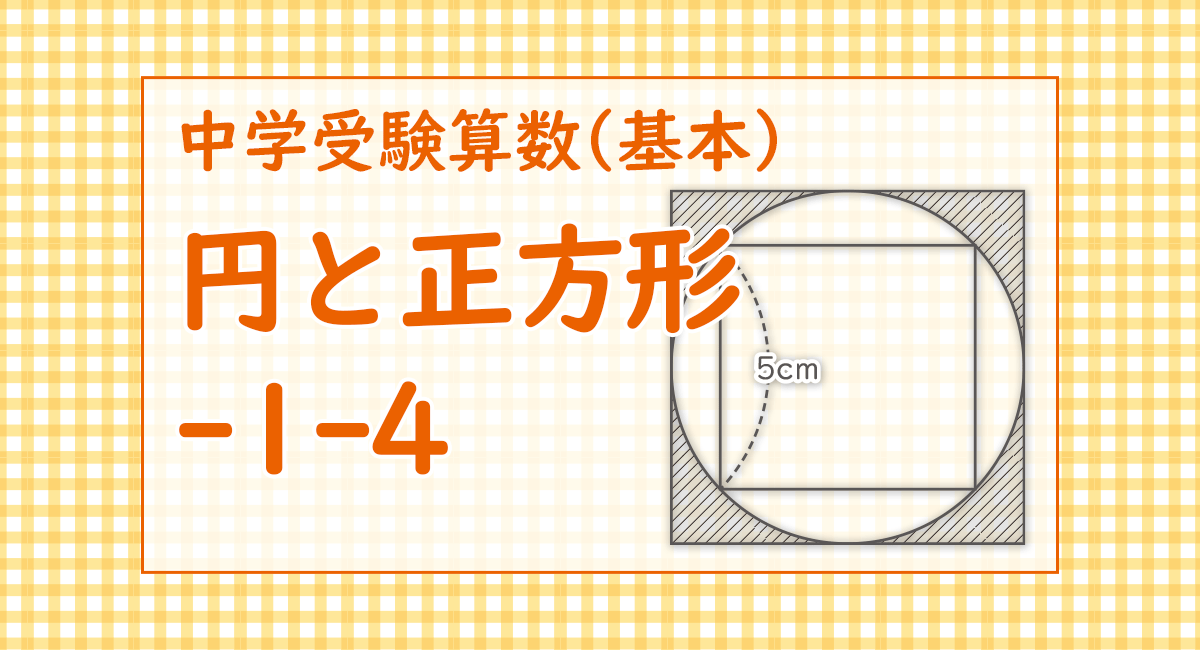
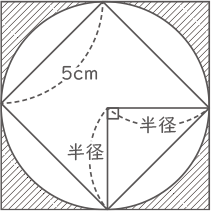
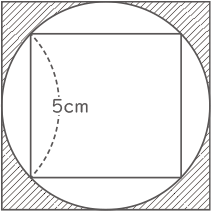 右の図のように,円の内側と外側に2つの正方形があり,内側の正方形の1辺の長さは5cmです。このとき,外側の正方形の面積は[ ① ]cm2で,斜線部分の面積は[ ② ]cm2です。ただし,円周率は3.14とします。
右の図のように,円の内側と外側に2つの正方形があり,内側の正方形の1辺の長さは5cmです。このとき,外側の正方形の面積は[ ① ]cm2で,斜線部分の面積は[ ② ]cm2です。ただし,円周率は3.14とします。
【家庭学習】問題集の画像も大きく見えて小さい文字もきれい
4.35
Amazonブランドのタブレット[Fire HD 10 Plus タブレット10.1インチ]フルHDディスプレイ(1920×1200)だから広くて見やすく家勉の必需品。
解答
- 解答を開く
-
 右の図のように,円の内側と外側に2つの正方形があり,内側の正方形の1辺の長さは5cmです。このとき,外側の正方形の面積は[ ① ]cm2で,斜線部分の面積は[ ② ]cm2です。ただし,円周率は3.14とします。
右の図のように,円の内側と外側に2つの正方形があり,内側の正方形の1辺の長さは5cmです。このとき,外側の正方形の面積は[ ① ]cm2で,斜線部分の面積は[ ② ]cm2です。ただし,円周率は3.14とします。 図の様に、内側の正方形を45度回転させると、外側の正方形の面積の半分が内側の正方形の面積であるとわかる。
図の様に、内側の正方形を45度回転させると、外側の正方形の面積の半分が内側の正方形の面積であるとわかる。
外側の正方形の面積=5×5×2=50cm2(①)。(円の半径×円の半径)は外側の正方形の面積の$ \displaystyle \frac{1}{4} $となるので50÷4=$ \displaystyle \frac{50}{4} $cm2。
よって、円の面積=(円の半径×円の半径)×3.14=$ \displaystyle \frac{50}{4} $×3.14
斜線部分の面積=外側の正方形の面積-円の面積=50-$ \displaystyle \frac{50}{4} $×3.14=50×(1-$ \displaystyle \frac{3.14}{4} $)=50×0.215=10.75cm2(②)。(答え) ① 50 ② 10.75
ではまた~


 図の様に、内側の正方形を45度回転させると、外側の正方形の面積の半分が内側の正方形の面積であるとわかる。
図の様に、内側の正方形を45度回転させると、外側の正方形の面積の半分が内側の正方形の面積であるとわかる。