
問題
問題(円が重なった面積)
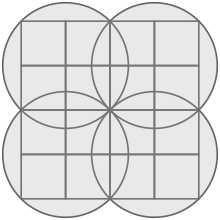
図の様に1辺が1cmの正方形16個を並べて大きな正方形を作り、さらに大きさの同じ円を4個重ねました。色の付いている部分の面積を求めなさい。ただし、円周率は3.14とします。
【2月1日の中学受験日】になる前に子供と旅に出よう、思い立った日に
4.17
人里離れた旅館?それとも海辺のリゾートホテル? 中学受験の前に一区切り、受験前最後の家族旅行はお早めに。今がそのチャンスかも。
解答
- 解答を開く
-
図の様に1辺が1cmの正方形16個を並べて大きな正方形を作り、さらに大きさの同じ円を4個重ねました。色の付いている部分の面積を求めなさい。ただし、円周率は3.14とします。


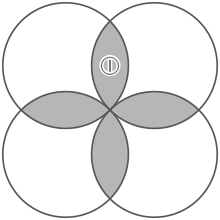
求める面積は、【円の面積×4-円の重なっている部分①の面積×4】となるので、①×4の面積を求める。
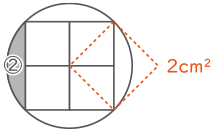
 破線の様な正方形を考えると、その1辺は半径と同じで、その面積は小さな正方形2個分なので2cm2となる。この2cm2は半径×半径と同じなので円の面積も求められる。
破線の様な正方形を考えると、その1辺は半径と同じで、その面積は小さな正方形2個分なので2cm2となる。この2cm2は半径×半径と同じなので円の面積も求められる。
円の面積=2×3.14=6.28cm2
色の付いた②の面積=(6.28-2×2)÷4=0.57
よって、①×4=②×8=0.57×8=4.56
求める面積=6.28×4-4.56=20.56(答え)20.56cm2
ではまた~


 破線の様な正方形を考えると、その1辺は半径と同じで、その面積は小さな正方形2個分なので2cm2となる。この2cm2は半径×半径と同じなので円の面積も求められる。
破線の様な正方形を考えると、その1辺は半径と同じで、その面積は小さな正方形2個分なので2cm2となる。この2cm2は半径×半径と同じなので円の面積も求められる。








