問題
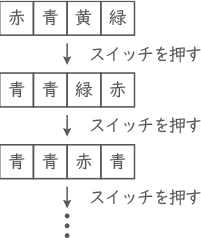赤，青，黄，緑の4色を点灯することができるライトを4つ，左から一列に並べます。この4つのライトは，スイッチを押すたびにある規則にしたがって色が切り替わります。例えば，右の固のように
赤を青，青を青，黄を緑，緑を赤
に切り替わるような規則を定めると，スイッチを押すたびに，この規則にしたがって色が変わっていきます。
はじめ，ライトは左から順に赤，青，黄，緑に点灯しています。
次の各問いに答えなさい。
（1） はじめの状態からスイッチを1回押したとき，異なる4色のライトが点灯するような規則は何通り作れますか。
（2） はじめの状態からスイッチを2回続けて押したとき，ライトが左から順に赤，青，黄，緑に点灯するような規則は何通り作れますか。
（3） はじめの状態からスイッチを3回続けて押したとき，4つのライトは初めて赤ー色になりました。このような規則は何通り作れますか。
人里離れた旅館？それとも海辺のリゾートホテル？ 中学受験の前に一区切り、受験前最後の家族旅行はお早めに。今がそのチャンスかも。
解答
- 解答を開く
-
赤，青，黄，緑の4色を点灯することができるライトを4つ，左から一列に並べます。この4つのライトは，スイッチを押すたびにある規則にしたがって色が切り替わります。例えば，右の固のように
赤を青，青を青，黄を緑，緑を赤
に切り替わるような規則を定めると，スイッチを押すたびに，この規則にしたがって色が変わっていきます。
はじめ，ライトは左から順に赤，青，黄，緑に点灯しています。
次の各問いに答えなさい。（1） はじめの状態からスイッチを1回押したとき，異なる4色のライトが点灯するような規則は何通り作れますか。
（2） はじめの状態からスイッチを2回続けて押したとき，ライトが左から順に赤，青，黄，緑に点灯するような規則は何通り作れますか。
（3） はじめの状態からスイッチを3回続けて押したとき，4つのライトは初めて赤ー色になりました。このような規則は何通り作れますか。
（1）
1つ目のライトは4色のどれでもよい。
2つ目のライトは残り3色のどれでもよい。
3つ目のライトは残り2色のどれでもよい。
4つ目のライトは残りの1色。
4×3×2×1＝24通り。（答え） 24通り
（2）
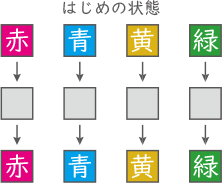
① 4つのライトとも色が変わらない場合
1通り。
② 3つのライトだけ色が変わらない場合
作れない。
③ 2つのライトだけ色が変わらない場合
色の変わらない２つを選ぶ選び方は、$ \displaystyle \frac{4×3}{2×1} $＝6通り。
残りの２つは色が変わるものだけが対象。（①の場合は除くため）
④ 1つのライトだけ色が変わらない場合
作れない。
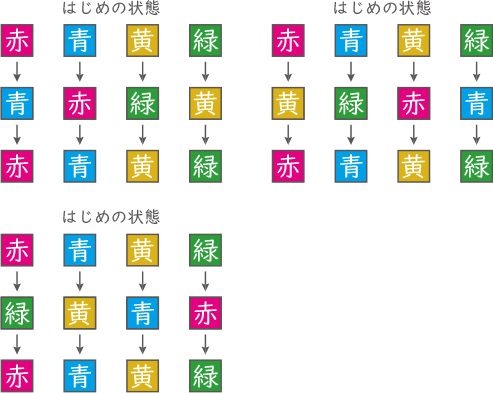
⑤ 4つのライトとも色が変わる場合
図の3通り。
合わせて、1＋6＋3＝10通り。（答え） 10通り
（3）
赤のライトはずっと赤のままで、以下の6通り。
（答え） 6通り
