問題
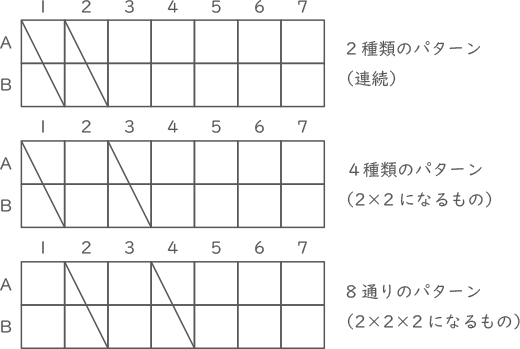
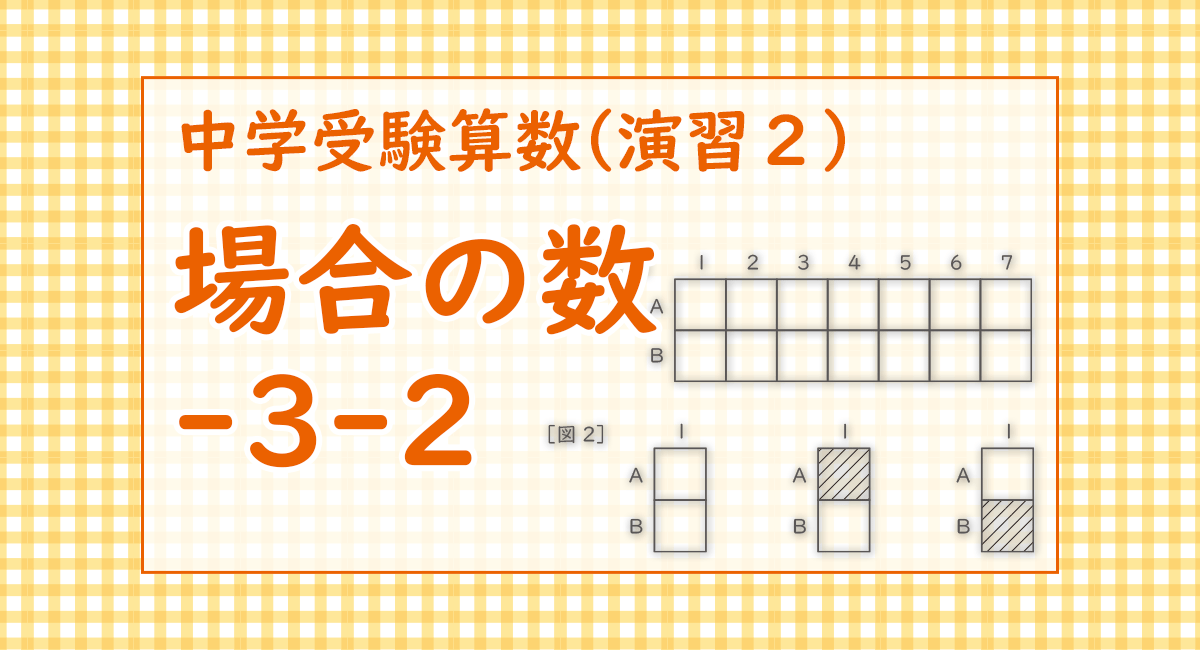
開成君は,図1 のような縦2 マス,横7 マスのマス目を用意し,マス目のいくつかを黒くぬりつぶして「暗号」を作ろうと考えました。そこで,次のようなルールを決め,何種類の暗号を作ることができるかを調べることにしました。
● 黒くぬりつぶすマス目は,上下左右が隣(とな)り合わないようにする。
● 読むときは,回したり裏返したりしない。
次の問いに答えなさい。
(1) 最大で何か所をぬりつぶすことができますか。その場合,暗号は何種類できますか。
(2) 14個のマス目のなかで5か所だけをぬりつぶす場合を考えます。
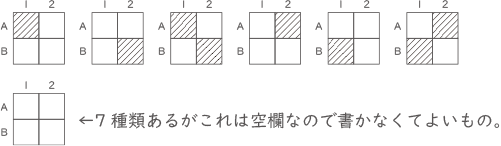
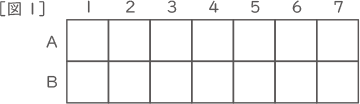
(ア)左から1列目と3列目のマス目をぬりつぶさないことにしてできる暗号をすべてかきなさい。黒くぬりつぶす部分は,次のページの図2のように斜線(しゃせん)を入れ,ぬりつぶす部分が分かるようにしなさい。また,解答らんはすべて使うとは限りません。使わない解答らんは,らん全体に大きく×印を入れて使わなかったことが分かるようにしなさい。(回答欄は問題末尾)
(イ)左から3列目と5列目のマス目をぬりつぶさないことにしてできる暗号は何種類ありますか。
(ウ)14個のマス目のなかで5か所だけをぬりつぶす場合,暗号は全部で何種類できますか。
(3) 左から1列目だけ,左から1列目と2列目の2列だけ,…と使う列の数を増やしながら,暗号が何種類できるかを考えようと思います。ただし,1マスもぬりつぶさない場合も1種類と数えることにします。たとえば,一番左の1列だけで考えると,暗号は図2の3種類ができます。
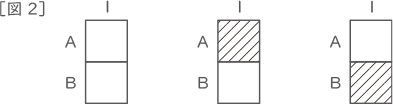
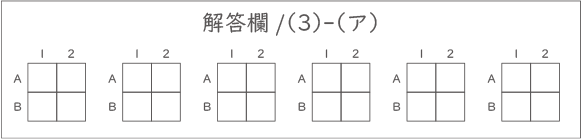
(ア) 左から2列だけを考えます。このときできる暗号のうち,1マスもぬりつぶさないもの以外をすべてかきなさい。解答らんはすべて使うとは限りません。使わない解答らんは,らん全体に大きく×印を入れて使わなかったことが分かるようにしなさい。(回答欄は問題末尾)
(イ) 左から1列目から3列目までの3列を考えます。このときできる暗号は何種類ありますか。
(ウ) 左から1列目から7列目までのマス目全部を使うとき,暗号は全部で何種類できますか。
これまでほとんどの通信教育で実現できなかった難関国私立中学合格。Z会なら、可能です。【公立中高一貫校を受検予定 】の方は試しに資料請求してみましょう。HPにも「小学生コース専科 公立中高一貫校受検対策講座のご案内」が詳しく記載されています。
解答
- 解答を開く
-
開成君は,図1 のような縦2 マス,横7 マスのマス目を用意し,マス目のいくつかを黒くぬりつぶして「暗号」を作ろうと考えました。そこで,次のようなルールを決め,何種類の暗号を作ることができるかを調べることにしました。
● 黒くぬりつぶすマス目は,上下左右が隣(とな)り合わないようにする。
● 読むときは,回したり裏返したりしない。次の問いに答えなさい。

(1) 最大で何か所をぬりつぶすことができますか。その場合,暗号は何種類できますか。
(2) 14個のマス目のなかで5か所だけをぬりつぶす場合を考えます。
(ア)左から1列目と3列目のマス目をぬりつぶさないことにしてできる暗号をすべてかきなさい。黒くぬりつぶす部分は,次のページの図2のように斜線(しゃせん)を入れ,ぬりつぶす部分が分かるようにしなさい。また,解答らんはすべて使うとは限りません。使わない解答らんは,らん全体に大きく×印を入れて使わなかったことが分かるようにしなさい。(回答欄は問題末尾)
(イ)左から3列目と5列目のマス目をぬりつぶさないことにしてできる暗号は何種類ありますか。
(ウ)14個のマス目のなかで5か所だけをぬりつぶす場合,暗号は全部で何種類できますか。(3) 左から1列目だけ,左から1列目と2列目の2列だけ,…と使う列の数を増やしながら,暗号が何種類できるかを考えようと思います。ただし,1マスもぬりつぶさない場合も1種類と数えることにします。たとえば,一番左の1列だけで考えると,暗号は図2の3種類ができます。

(ア) 左から2列だけを考えます。このときできる暗号のうち,1マスもぬりつぶさないもの以外をすべてかきなさい。解答らんはすべて使うとは限りません。使わない解答らんは,らん全体に大きく×印を入れて使わなかったことが分かるようにしなさい。(回答欄は問題末尾)
(イ) 左から1列目から3列目までの3列を考えます。このときできる暗号は何種類ありますか。
(ウ) 左から1列目から7列目までのマス目全部を使うとき,暗号は全部で何種類できますか。

(1)

(答え) 7か所 2種類
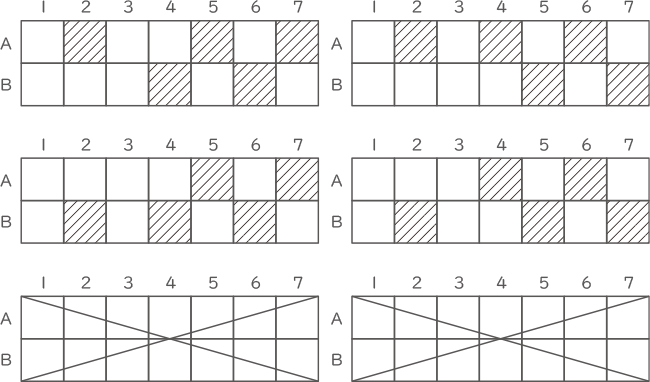
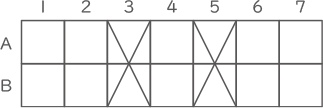
(2)-(ア)
(答え)

 (2)-(イ)
(2)-(イ)
1・2列目で2種類作れる。
4列目で2種類作れる。
6・7列目で2種類作れる。
全部で2×2×2=8種類。(答え) 8種類
(2)-(ウ)
14個のマス目のなかで5か所だけをぬりつぶす→いずれかの2列はぬりつぶさない
7列のうち5列を選ぶ選び方は$ \displaystyle \frac{7×6×5×4×3}{5×4×3×2×1} $=21通り。
ぬりつぶさない列の組み合わせと、そのときの種類

(答え) 102種類
(3)-(ア)
【2列だけのとき】(答え)

(3)-(イ)
【3列だけのとき】
9+4+4=17種類
(答え) 17種類
(3)-(ウ)
【4列だけのとき】
21+10+10=41種類
【5列だけのとき】

51+24+24=99種類
【6列だけのとき】

123+58+58=239種類
【7列全てのとき】

297+140+140=577種類
(答え) 577種類


 (2)-(イ)
(2)-(イ)