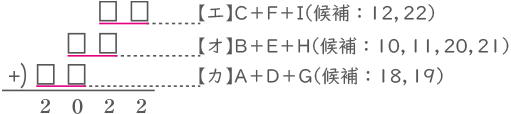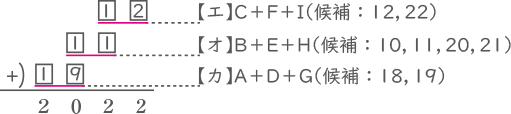問題
下の会話文中の【ア】から【ク】にあてはまる数を答えなさい。ただし,答えが複数ある場合はすべて答えなさい。
X:「下の筆算が成り立つように,各アルファベットに0から9までの数を1つずつ入れることを考えよう。」
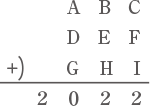
Y:「それなら簡単だよ。AとDとGが6で,BとEとHが7で,CとFとIが4ならば,674+674+674=2022が成り立つよ。」
X:「そうだね。では,同じ数が使えなかったらどうだろう。各アルファベットに入る数が異なるように,0から9までの数を1つずつ入れられるかな。まず,一の位の数のみに着目すると,C+F+Iとして考えられる値は何があるだろうか。」
Y:「【ア】が考えられるね。」
X:「次に,繰(く)り上(あ)がりと十の位の数のみに着目してB+E+Hの値を考えてみよう。」
Y:「【イ】が考えられるね。同じようにしてA+D+Gの値は【ウ】が考えられるよ。」
X:「これだけだと,まだ各位の数の和の候補が多くて決められないね。でも,各アルファベットには0から9までの中から異なる9つの数が入ることを考えると,各位の数の和の組合せは1通りに絞(しぼ)られるんじゃないかな。」
Y:「C+F+I=【エ】,B+E+H=【オ】,A+D+G=【カ】だね。ということは,0から9の中で使わない数は【キ】なんだね。」
X:「では,Aが7のとき,残りのアルファベットに入る数の組合せが何通りあるか求めてごらん。」
Y:「わかった。【ク】通りだね。」
試験で使われる問題用紙はかなり大きめ。同じ大きさで過去問を用意して本番感覚を養いましょう。印刷するのはパパとママの役目。A3ノビまで対応、全色顔料インクで滲まない。最大給紙枚数は550枚。
解答
- 解答を開く
-
下の会話文中の【ア】から【ク】にあてはまる数を答えなさい。ただし,答えが複数ある場合はすべて答えなさい。
X:「下の筆算が成り立つように,各アルファベットに0から9までの数を1つずつ入れることを考えよう。」

Y:「それなら簡単だよ。AとDとGが6で,BとEとHが7で,CとFとIが4ならば,674+674+674=2022が成り立つよ。」
X:「そうだね。では,同じ数が使えなかったらどうだろう。各アルファベットに入る数が異なるように,0から9までの数を1つずつ入れられるかな。まず,一の位の数のみに着目すると,C+F+Iとして考えられる値は何があるだろうか。」
Y:「【ア】が考えられるね。」
X:「次に,繰(く)り上(あ)がりと十の位の数のみに着目してB+E+Hの値を考えてみよう。」
Y:「【イ】が考えられるね。同じようにしてA+D+Gの値は【ウ】が考えられるよ。」
X:「これだけだと,まだ各位の数の和の候補が多くて決められないね。でも,各アルファベットには0から9までの中から異なる9つの数が入ることを考えると,各位の数の和の組合せは1通りに絞(しぼ)られるんじゃないかな。」
Y:「C+F+I=【エ】,B+E+H=【オ】,A+D+G=【カ】だね。ということは,0から9の中で使わない数は【キ】なんだね。」
X:「では,Aが7のとき,残りのアルファベットに入る数の組合せが何通りあるか求めてごらん。」
Y:「わかった。【ク】通りだね。」
【ア】・・・C+F+Iとして考えられる値
C+F+Iの和の一の位が2となるのは、12と22のとき。(答え) 12,22
【イ】・・・B+E+Hの値
一の位から1または2が繰り上がるので、
B+E+Hの和の一の位が2となるのは、10,20,11,21のとき。(答え) 10,11,20,21
【ウ】・・・A+D+Gの値
十の位から1または2が繰り上がるので、
A+D+Gの和の一の位が0となるのは、19,18のとき。(答え) 18,19
【エ】・・・C+F+I(候補:12,22)
【オ】・・・B+E+H(候補:10,11,20,21)
【カ】・・・A+D+G(候補:18,19)
1から9までの和は45なので【エ】+【オ】+【カ】は45以下となる。
【カ】は18か19のどちらかなので、45-18=27より、【エ】の22と【オ】の20と21は不適切。(和が27を超えるので)
よって、【エ】は12となる。そのときに適切な【オ】は11の1つだけ。さらに適切な【カ】は19となる。
(答え) 【エ】12, 【オ】11, 【カ】19
【キ】・・・使わない数
45-(12+11+19)=3(答え) 3
【ク】・・・Aが7のとき,残りのアルファベットに入る数の組合せが何通りあるか
Aが7のとき、A(7)+D+G=19より、D+G=12。
残りの数のうち12を作れるのは4と8なので、(D,G)=(4,8)または(8,4)の2通り。さらに残りの数より、
B+E+H=11となるのは(0,2,9)または(0,5,6)の組み合わせ。
C+F+I=12となるのは(1,2,9)または(1,5,6)の組み合わせ。
ただし、(B,E,H)が(0,2,9)のとき(C,F,I)は(1,5,6)となり、(B,E,H)が(0,5,6)のとき(C,F,I)は(1,2,9)となる。(0,2,9)、(1,5,6)、(0,5,6)、(1,2,9)のどれも、並び方の総数は6通りずつ。
(D,G)が2通り×(0,2,9)が6通り×(1,5,6)が6通り
と、
(D,G)が2通り×(0,5,6)が6通り×(1,2,9)が6通り2×6×6+2×6×6=144通り。
(答え) 144通り