問題
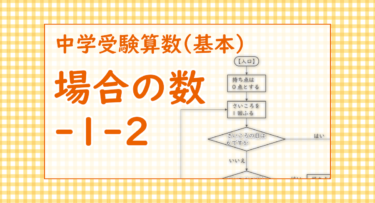
さいころをふって得点していくゲームを考えます。下の図は、【入口】から【出口】まで矢印の方向に進みます。このとき、次の問いに答えなさい。
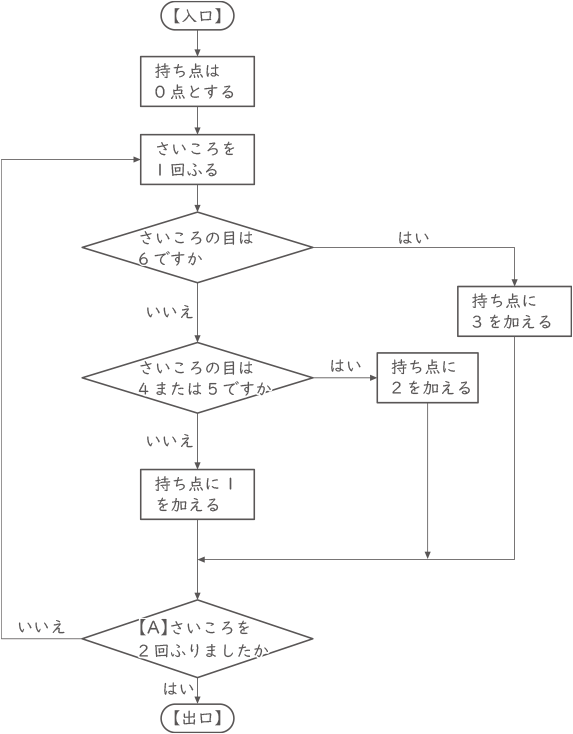
(1) 【出口】で持ち点が3点になるような、さいころの目の出方は全部で何通りありますか。
(2) 【出口】での持ち点は全部で何通りありますか。
(3) 【A】を「さいころを3回ふりましたか」に変更します。このとき、【出口】での1番高い持ち点と1番低い持ち点の差は何点になりますか。
(4) 【A】を「さいころを4回ふりましたか」に変更します。このとき、【出口】での持ち点が10点になるような、さいころの目の出方は全部で何通りありますか。
これまでほとんどの通信教育で実現できなかった難関国私立中学合格。Z会なら、可能です。【公立中高一貫校を受検予定 】の方は試しに資料請求してみましょう。HPにも「小学生コース専科 公立中高一貫校受検対策講座のご案内」が詳しく記載されています。
解答
- 解答を開く
-
さいころをふって得点していくゲームを考えます。下の図は、【入口】から【出口】まで矢印の方向に進みます。このとき、次の問いに答えなさい。

(1) 【出口】で持ち点が3点になるような、さいころの目の出方は全部で何通りありますか。
(2) 【出口】での持ち点は全部で何通りありますか。
(3) 【A】を「さいころを3回ふりましたか」に変更します。このとき、【出口】での1番高い持ち点と1番低い持ち点の差は何点になりますか。
(4) 【A】を「さいころを4回ふりましたか」に変更します。このとき、【出口】での持ち点が10点になるような、さいころの目の出方は全部で何通りありますか。(1)
この条件分岐する図はフローチャートと呼ばれている。
このフローチャートから分かることは、
・サイコロは2回ふったら終わりになる
・1回ふるごとに必ず1点か2点か3点のどれかが加えられる
・6の目では3点、4か5の目では2点、1か2か3の目では1点が加えられる2回ふって3点になるのは、
1回目が1点(目が1か2か3)→2回目が2点(目が4か5)・・・3×2=6通り
1回目が2点(目が4か5)→2回目が1点(目が1か2か3)・・・2×3=6通り
合わせて6+6=12通り。(答え) 12通り
(2)
6点(3+3)
5点(3+2、2+3)
4点(3+1、2+2、1+3)
3点(2+1、1+2)
2点(1+1)
以上の5通り(答え) 5通り
(3)
1番高い持ち点は3+3+3=9点
1番低い持ち点は1+1+1=3点
差は6点(答え) 6点
(4)
10点になるのは、【3点が3回と1点が1回の時】、【3点が2回と2点が2回の時】の2つ。【3点が3回と1点が1回の時】
・3点が出るのは目が6の時、1点が出るのは目が1か2か3の時(1×1×1×3通り)
・3,3,3,1の出かた(並び順)は4通り
よって、3×4=12通り。【3点が2回と2点が2回の時】
・3点が出るのは目が6の時、2点が出るのは目が4か5の時(1×1×2×2通り)
・3,3,2,2の出かた(並び順)は6通り
よって、4×6=24通り。合わせて12+24=36通り。
(答え) 36通り